Felhasználói eszközök
Tartalomjegyzék
6. Nemlineáris egyenletek numerikus megoldása
6.1. Algebrai egyenletek
6.2. Polinomok zérus-helyeinek korlátai
6.3. Lobacsevszkij-féle módszer
6.4. Intervallumfelező eljárás
6.5. Húrmódszer
6.6. Newton-Raphson (érintő) módszer
6.7. Szelőmódszer.
6.8. Érintő és húr módszerek közös alkalmazása
6.9. Fixpont iterációs módszer (Fokozatos közelítési módszer)
Bevezetés
A matematika különböző egyenletekkel és egyenletrendszerekkel foglalkozik. Azok a legegyszerűbb egyenletek, melyekben az ismeretlenek numerikus értékeket vehetnek fel. Bonyolultabb esetekben az ismeretlenek vektorok (egyenletrendszerekben), függvények (differenciálegyenletekben, integrálegyenletekben, funkcionális egyenletekben) lehetnek. Az egyenletek a matematika egyik legfontosabb objektumait alkotják. Sok gyakorlati és tudományos probléma olyan változókat tartalmazz, melyeknek nem lehet megmérni az értékeit, vagy kész képletek alapján kiszámítani. Ilyen esetben az lehet a megoldás, hogy a változók közti kapcsolatokat egyenletek segítségével leírják. Ha megoldjuk az egyenletet (vagy egyenletrendszert), akkor sikerült matematikailag meghatározni az ismeretleneket, és végeredményben megoldani a megfelelő gyakorlati vagy tudományos problémát. A továbbiakban a
$$f(x)=0\tag{6.1}\label{eq:6.1}$$
alakú egyenlet megoldásának módszereivel foglalkozunk.
A $\eqref{eq:6.1}$ egyenletet analitikus, képletbe foglalható megoldását az esetek többségében nem lehet megvalósítani. Ezért fontos szerepe van a numerikus módszereknek, amelyekkel tetszőleges pontosságú, de „csak” a közelítő megoldást lehet elérni. A gyakorlati problémák szempontjából ez nem jelent hátrányt, mivel a konkrét feladatokban az adatok mindig hibákat tartalmaznak (pl. a mérési hiba),és még a képletek kiértékelésekor is csak közelítő értéket kaphatunk. Például, a Cardano-formula $\eqref{eq:6.10}$ alkalmazásánál közelítő értékeket kapunk.
Ezért a közelítő megoldás, ha azt a megfelelő pontossággal állítottuk elő, a gyakorlati felhasználásban teljesen elfogadható.
A $\eqref{eq:6.1}$ $x_k$ a $ε$ pontosságú közelítő megoldása (gyöke) azt jelenti, hogy az $x^*$ pontos megoldás a $x_k ε >0$ sugarú környezetében van
$$|x^* - x_k|<ε\tag{6.2}\label{eq:6.2}$$
ahol ε egy előre megadott érték (megengedett hiba), az $(x_k -ε, x_k +ε)$, az un. bizonytalansági intervallum. A legtöbb numerikus módszernek az a közös jellemzője, hogy azok iterációkat (többször végrehajtott közelítéseket) tartalmaznak. Az iterációs módszereknek az a sajátossága, hogy induláskor meg kell adni a megoldás kezdő (első közelítő) értékét $x_0$-t, vagy az $(a, b)$ intervallumot, mely tartalmazza a gyököt. A módszertől függően a $x_0$ érték alapján meg lehet állapítani a gyök következő $x_1$ közelítését. Az iterációt addig kell folytatni, amíg nem kapjuk meg a megfelelő pontosságú megoldást, vagy nem állapítjuk meg, hogy az adott módszerrel nem tudjuk megoldani az egyenletet. Mivel az iterációs módszer alkalmazása előtt meg kell adni a $x_0$ értékét vagy az $(a, b)$ intervallumot, ezért végre kell hajtani egy előkészítő szakaszt, amelyben megállapítjuk ezeket az értékeket. A legegyszerűbb lehetőség az egyenletek grafikus megoldásának az alkalmazása. E célból az egyenletet két alakban lehet előállítani:
- A $\eqref{eq:6.1}$ függvény grafikonja alapján közelítőleg megállapítjuk a függvény zérus-helyeit.
- Átalakítjuk a $\eqref{eq:6.1}$ egyenletet
$$h(x) = g(x)\tag{6.3}\label{eq:6.3}$$
A $h(x)$ és a $g(x)$ függvényeket ugyanabban a koordinátarendszerben ábrázoljuk, és a függvények görbéinek metszéspontjaihoz tartozó $x$ értékek adják az egyenlet megoldását.
A Maxima segítségével mind a két esetben ez könnyen megoldható.
6.1. Példa
$$x^2 - 2 - \sin x =0$$
$$x^2 - 2= \sin x$$
Kísérletezhetünk a Maxima-ban különböző intervallumok kiválasztásával.
wxplot2d([x^2-4,sin(x)],[x,-5,5],[style,[lines,7,1],[lines,7,2]]);

wxplot2d([x^2-4,sin(x)],[x,-3,1],[style,[lines,7,1],[lines,7,2]]);

wxplot2d([x^2-4,sin(x)],[x,1.5,2.5],[style,[lines,7,1],[lines,7,2]]);
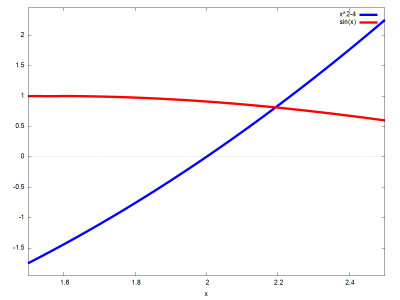
6.1. Algebrai egyenletek
Ha az egyenletben szereplő függvény algebrai (racionális vagy irracionális), akkor a $\eqref{eq:6.1}$ algebrai egyenlet. Az algebrai egyenleteket kanonikus alakban lehet átalakítani (de nem garantált, hogy ezek az egyenletek ekvivalensek lesznek)
$$a_0 x^n + a_1 x^{n-1} + a_2 x^{n-2} + … + a_{n-1} x+ a_n=0 \tag{6.4}\label{eq:6.4}$$
A $\eqref{eq:6.4}$(6.4) egyenlet bal oldala $p(x)$ $n$-ed fokú polinom:
$$p(x)=a_0 x^n + a_1 x^{n-1} + a_2 x^{n-2} + … + a_{n-1} x+ a_n \tag{6.5}\label{eq:6.5}$$
A $\eqref{eq:6.5}$(6.5) egyenlet ritkán oldható meg analitikus módszerrel.
6.2. Példa
$$\frac{x-1+\sqrt{x^2-6}}{3(x-2)}=1+\frac{x-3}{x}$$
$$x(x-1+\sqrt{x^2-6})=3x(x-2)+3(x-2)(x-3)$$
$$x^2-x+x\sqrt{x^2-6}=3x^2-5x+3x^2-15x+18$$
$$x\sqrt{x^2-6}=5x^2-20x+18$$
$$x^2 (x^2 - 6) = 25 x^4 - 200 x^3 +580 x^2 - 720x +324$$
$$24 x^4 - 200 x^3 +586 x^2 - 720x +324 = 0$$
A másodfokú egyenlet
$$ax^2 + bx +c =0 \tag{6.6}\label{eq:6.6}$$
gyökei
$$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \tag{6.7}\label{eq:6.7}$$
alakban adhatók meg, Ezek a gyökök általános esetben komplex számok
A 16. században a matematikusok nagy erőfeszítéseket tettek a 3- és 4-fokú egyenletek megoldására. De akkor még nem vették figyelembe a negatív számokkal, és ezért kénytelenek voltak külön-külön vizsgálni a
$$x^3 +px =q\tag{6.8}\label{eq:6.8}$$
$$x^3 +q =px\tag{6.9}\label{eq:6.9}$$
egyenleteket. A $\eqref{eq:6.9}$ egyenletet C. Del-Ferro (1465-1526) olasz matematikus megoldotta, és azt A Fiore nevű tanítványával közölte. Fiore matematikai párbajra hívta ki N. Tartalya-t, aki a matematikát csak autodidakta módon tanulta. Néhány nappal a párbaj előtt Tartalya megtalálta a harmadfokú egyenlet általános megoldását és ezzel megnyerte a párbajt.
$$x=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} +\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} \tag{6.10}\label{eq:6.10}$$
Mivel a megoldást Tartalya-tól megtudta D Cardano (1501-1576), aki nyilvánosságra hozta ezt az eredményt, ezért az a matematika történetébe a
Cardano-képlet nevén került.
A harmadfokú egyenlet megoldása:
$$ax^3 + bx^2 + cx +d =0\tag{6.11}\label{eq:6.11}$$
Átalakítás után a $\eqref{eq:6.11}$ formula, a
$$y =\frac{x+b}{3a} \tag{6.12}\label{eq:6.12}$$
helyettesítés alkalmazásával
$$y^3 +3px + 2q =0 \tag{6.13}\label{eq:6.13}$$
alakra hozható, ahol
$$p = \frac{1}{9}\cdot\frac{(3ac – b^2)}{a^2}, \quad q =\frac{1}{2}\left(\displaystyle\frac{3b^3}{27a^3}-\displaystyle\frac{ bc}{3a^2}+\displaystyle\frac{d}{a} \tag{6.14}\label{eq:6.14}\right)$$
A $\eqref{eq:6.13}$ egyenlet valós gyökeinek száma a
$$D = q^2 + p^3$$
diszkrimináns alapján állapítható meg. Ha $D>0$, akkor az egyenletnek egy valós gyöke van,
Ha $D<0$, akkor az egyenletnek három valós gyöke van,
Ha $D=0$, és ($p=q=0$), akkor három valós egybeeső gyöke van ($x=0$),
Ha $D=0$, és ($p^3=-q^2 ≠0$), akkor három valós gyöke van melyből kettő egybeeső.
Az egyenlet megoldásának lehetőségei:
a) Felbontás szorzatokra
$$ax^3 + bx^2 + cx +d =0$$
$$ax^3 + bx^2 + cx +d =a (x -x_1) (x -x_2) (x -x_3) $$
(gyöktényezős alakra hozás)
Például,
$$x^3 +x^2 - 6x =0$$
$$x^3 +x^2 - 6x =x (x - 2)(x+3)=0$$
Akkor:
$$x_1 =0,\quad x_2 =2, \quad x_3= -3.$$
b) Cardano-formula
$$ax^3 + bx^2 + cx +d =0$$
$$y_1= u +v y_2 =e_1 u+e_2 v y_3 =e_2 u + e_1 v$$
ahol
$$u=\sqrt[3]{-q+\sqrt{q^2+p^3}}$$
$$v=\sqrt[3]{-q-\sqrt{q^2+p^3}}$$
és
$e_1$ , $e_2$ a
$$x^2 + x +1 =0$$
egyenlet megoldásai:
$$e_1=-\frac{1}{2}+i\frac{\sqrt{3}}{2}$$
$$e_1=-\frac{1}{2}-i\frac{\sqrt{3}}{2}$$
6.3. Példa
$$y^3 + 6y^2 + 2 =0$$
$$p =2,\quad q =1,\quad q^2 +p^3 =9$$
$$u=\sqrt[3]{-1+3}=\sqrt[3]{2}=1,\!2599 $$
$$v=\sqrt[3]{-1-3}=\sqrt[3]{-4}=-1,\!5874 $$
$$y_1 =u +v = -0,\!3275$$
$$y_2=-\frac{1}{2}(u+v)+i\frac{\sqrt{3}}{2}(u-v)= -0,\!1638+i\cdot2,\!4659$$
$$y_3=-\frac{1}{2}(u+v)-i\frac{\sqrt{3}}{2}(u-v)= -0,\!1638-i\cdot2,\!4659$$
c) A gyökök és együtthatók összefüggése alapján:
$$x_1+x_2+x_3= -\frac{b}{a}$$
$$\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}= -\frac{c}{d}$$
$$x_1x_2x_1 = -\frac{d}{a}$$
Cardano tanítványának L. Ferrarinak (1522-1565) sikerült megoldani bizonyos negyedfokú egyenleteket. Az algebrai szimbolika (jelölésrendszer) létrehozásával és a szám fogalmának általánosításával a komplex számok segítségével, a 17.-18. századokban lehetőség nyílt a magasabb fokú algebrai egyenletek és polinomok tulajdonságainak tanulmányozására. Az egyik legaktuálisabb probléma az ötödfokú egyenlet megoldásának megtalálása volt. A 17. század végén és a 18. század elején bebizonyították, hogy az ötödfokú egyenlet gyökeinek meghatározására nem létezik formula. (A Ruffini-Abel tétel szerint (1799) a négynél magasabb fokú egyenletnek nincs analitikus megoldása). Ez az eredmény három tudós, a Lagrange G. (1736-1813), az olasz P. Ruffini (1765-1822), és a fiatal norvég N. Abel nevéhez fűződik. A probléma a francia E. Galois által nyert teljes megoldást, mivel Galois létrehozott olyan elméletet, amelynek segítségével megállapítható, hogy az egyenlet gyökei radikálok segítségével kifejezhetők. Felszínre került az algebrai egyenletek gyökei létezésének problémája. A 18. században G.D'Alembert bebizonyította, hogy minden algebrai egyenletnek van legalább egy komplex gyöke. A bizonyítás bizonyos hiányosságot tartalmazott, melyet később Gauss kiküszöbölt, és ezért ez a tétel az irodalomban gyakran Gauss neve alatt szerepel. A tétel kimondja, hogy $n$-ed fokú egyenletnek $n$ komplex gyöke van.
6.2. Polinomok zérus-helyeinek korlátai
Abszolút gyökkorlát
Megfogalmazunk egy egyszerű korlátot, amelyen kívül a polinom nem tartalmazhat gyököket.
Legyen
$$p(x)=a_0 x_n + a_1 x_{n-1} + a_2 x_{n-2} + … + a_{n-1} x+ a_n \tag{6.15}\label{eq:6.15}$$
Mivel
$$\lim_{x\to\infty}p(x)=\infty,\tag{6.16}\label{eq:6.16}$$ (6.16)
akkor létezik olyan $K$, amelynél az $a_0$ főegyüttható meghatározza a polinom értékének előjelét és ettől nagyobb $x$ értékekre biztosan már nem lehet gyök.
Bizonyítás.
Legyen
$$|a_0 x^n | >| a_1 x^{n-1} + a_2 x^{n-2} + … + a_{n-1} x+ a_n|$$
Átalakítjuk a jobb oldali kifejezést:
$$| a_1 x^{n-1} + a_2 x^{n-2} + … + a_{n-1} x+ a_n| \leqslant | a_1 x^{n-1} |+ |a_2 x^{n-2} |+ … + |a_{n-1} x|+ |a_n| \leqslant $$
$$A| x^{n-1} |+ A|x^{n-2} |+ … + A| x|+ A$$
ahol
$$A = \max(| a_1 | , | a_2 | ,… | a_n|)$$
$$A| x^{n-1} |+ A|x^{n-2} |+ … + A| x|+ A = A\frac{| x^{n-1} |+|x^{n-2} |+ … + | x|+ 1) = A (| x^n | –1}{| x| –1}$$
mint mértani sorozat összege.
$$A\frac{|x|^n–1}{|x|-1} < A\frac{|x|^n}{|x|-1} <|a_0||x|^n$$
legyen $|x|>1$, rendezés után az egyenlőtlenség megoldása:
$$|x|> 1 + \frac{A}{| a_0|} =K \tag{6.17}\label{eq:6.17}$$
Tehát a polinom valós gyökeinek a $(-K, K)$ intervallumban kell elhelyezkedni.
6.4. Példa
Állapítsuk meg a
$$p(x)= x^5 +2 x^4 -5 x^3 +8 x^2 -7x -3$$
polinom gyökeinek korlátait!
$$|a_0| =1,\quad A =8,\quad K=\frac{8}{1} +1 =9,$$
A gyököket a $[-9, 9]$ intervallumban kell keresni!
Pozitív gyök-korlát
Egy polinomnak csak akkor van pozitív gyöke, ha $a_0>0$ és az együtthatói között van legalább egy negatív, vagy ha $a_0<0$ és a polinom együtthatói között van legalább egy pozitív).
Legyen $a_0>0$, és $B$ a negatív együtthatók abszolút értékei közül a maximális, és $k$ az első negatív együttható indexe (nullával kezdődik). Akkor a pozitív gyökkorlát a következő képlet alapján számítható ki:
$$N=\sqrt[k]{\frac{B}{a_0}}+1\tag{6.18}\label{eq:6.18}$$
Bizonyítás.
Tételezzük fel, hogy $x>1$. A polinomot helyettesítjük egy vele azonos viselkedésű, de kisebb helyettesítési értékeket szolgáltató polinommal:
$$a_0 x^n + a_1 x^{n-1} + a_2 x^{n-2} + … + a_{n-1} x+ a_n \geqslant a_0 x^n - B( x^{n-k} + x^{n-k-1} + … + x+1) = a_0 x^n - B\frac{ x^{n-k+1} - 1}{x - 1}$$
Ezt úgy állítottuk elő, hogy az $a_1, a_2, …, a_{k-1}$ együtthatókat nullával, az $a_k, a_{k+1}, …, a_n$ értékeket ($-B$) -vel helyettesítettük.
$$a_0 x^n - B\frac{x^{n-k+1}+1}{x – 1} > a_0 x^n -B\frac{x^{n-k+1}}{x - 1} = \frac{x^{n-k+1}}{x - 1}[ a_0 x^{k-1}(x - 1) - B ] \geqslant 0$$
miután
$$x>1,\quad \frac{x^{n-k+1}}{x - 1}>0,$$
ebből következik, hogy
$$a_0 x^{k-1}(x - 1) - B\geqslant 0$$
$$a_0 x^{k-1}(x - 1) - B > a_0 (x -1)^{k-1}(x - 1) - B = a_0 (x -1)^k- B\geqslant 0$$
Ebből
$$(x-1)^k \geqslant \frac{B}{a_0} $$
és
$$x\geqslant\sqrt[k]{\frac{B}{a_0}}+1=N$$
Ha a polinom nem tartalmaz negatív együtthatót, akkor annak nincs pozitív gyöke.
6.5. Példa
$$p(x)= x^5 +2 x^4 -5 x^3 +8 x^2 -7x -3$$
$$a_0 =1,\quad B =7,\quad k =2,\quad N=3,\!64$$
A gyökök a $[-9; 3,\!64]$ intervallumon vannak elhelyezve.
Gyökök további elhelyezkedéséről
A pozitív gyökkorlát számítása alapján lehetőség nyílik a gyökök további elhelyezkedésének vizsgálatára. A $p(x)$ polinomhoz szerkeszthetünk három olyan segéd-polinomot, amelyek pozitív gyökkorlátai az eredeti polinom pozitív és negatív gyökeinek intervallumait meghatározzák.
Legyen
$$p_1(x) =x^np\left(\frac{1}{x}\right)\tag{6.19}\label{eq:6.19}$$
segéd-polinom pozitív gyökkorlátja $N_1$.
$$p_2(x) = p(-x) \tag{6.20}\label{eq:6.20}$$
segéd-polinom pozitív gyökkorlátja $N_2$,
$$p_3(x) =x^np\left(-\frac{1}{x}\right) \tag{6.21}\label{eq:6.21}$$
segéd-polinom pozitív gyökkorlátja $N_3$.
Az eredeti polinom pozitív gyökei az $\left[\displaystyle\frac{1}{N_1}, N\right]$, a negatív gyökök a $\left[-N_2, -\displaystyle\frac{1}{N_3}\right]$, intervallumban lehetnek.
Bizonyítás.
Legyen $a_{+}$ az eredeti $p(x)$ polinom egy pozitív gyöke, akkor $a_{+}<N$ és miután $\displaystyle\frac{1}{a_{+}}$ gyöke a $p_1(x)$ -nek $\displaystyle\frac{1}{a_{+}}<N $ , és így ebből következik a
$$\frac{1}{N} <a_{+} < N$$
állítás. Hasonlóan látható be a
$$\frac{1}{N^2} <a_{-} <\, –\frac{1}{N^3}$$
ahol a $a_{-}$ a $p(x)$ polinom egy negatív gyökét jelöli.
Megjegyzés: Ha a $p_2 (x)$ polinomnak nincs pozitív gyöke, akkor a $p(x)$-nek nincs negatív gyöke, ha $p(x)$-nek nincs pozitív gyöke, de meghatározható a $N_2$, akkor van negatív gyöke.
A gyökkorlátok meghatározására más tételek is ismertek:
6.1. Tétel
Legyen
$$a = \max \{ |a_1|, |a_2|, …, |a_n|\} \tag{6.22}\label{eq:6.22}$$ (6.22)
és
$$A = \max \{ |a_0|, |a_1|, …, |a_{n-1}|\} \tag{6.23}\label{eq:6.23}$$ (6.23)
akkor mindegyik $x_i$ gyökre igaz:
$$\frac{|a_n|}{A+|a_n|}\leqslant x_i \leqslant 1 +\frac{a}{|a_0|} \tag{6.24}\label{eq:6.24}$$
6.2. Tétel (Newton-tétel).
Ha
$$p(c)>0,\quad p^\prime(c)>0,\quad\ldots, \quad p^{(n)}(c)>0, \tag{6.25}\label{eq:6.25}$$ akkor a
$$p(x) =0$$
egyenlet gyökeire teljesül a következő egyenlőtlenség:
$$x_i < c$$
Polinomok valós gyökeinek közelítése Sturm sorozattal
Legyen
$$f(x)=a_0 x^n + a_1 x^{n-1} + a_2 x^{n-2} + … + a_{n-1} x+ a_n = 0 \tag{6.26}\label{eq:6.26}$$
Tételezzük fel, hogy a polinomnak nincs többszörös gyöke.
Használjuk a következő eljárást – az Euklidészi osztási algoritmus változata:
$$f_0 (x):=f(x),$$
$$f_1 (x):=f′(x),$$
$$f_{j-1}(x)=q_{j-1}(x)f_j(x)-f_{j+1}(x), \quad j=1,2,...,m-1$$
$$f _{m-1}(x)=q_{m-1}(x) f_m(x)\tag{6.27}\label{eq:6.27}$$
ahol az $f_{j+1}(x)$ maradék polinom fokszáma kisebb az $f_j(x)$ osztó polinom fokszámánál. Mivel a
$$f_0(x), f_1 (x), f_2 (x), ….\tag{6.28}\label{eq:6.28}$$
polinomok fokszámai monoton csökkennek, eljutunk egy olyan $f_m (x)$ -hez, amely már osztója a $f_{m-1}(x)$ polinomnak.
Lemma.
Ha $f(x)$ polinomnak a véges $[a, b]$ intervallumba eső gyökei egyszeresek, akkor
a) minden $x∈ [a,b]$ -re $f_m (x)≠0$,
b) ha valamely $1\leqslant j<m$-re és $x∈ [a,b]$-re
$$f_j(x) =0$$
akkor
$$f_{j-1}(x) f_{j+1}(x) < 0$$
c) ha valamely $x∈ [a,b]$-re $f_1(x)=0$, akkor
$$f_0 (x)f_1 (x)>0$$
(a szorzatfüggvény növekvő az $x$ helyen)
Definíció. Legyen
$$f_0(x), f_1 (x), …, f_m (x)\tag{6.29}\label{eq:6.29}$$
valós együtthatós polinomoknak olyan sorozata, amelyben a fokszámok monoton csökkennek. Ezt Sturm-sorozatnak nevezzük a $[a, b]$ intervallumon, ha a Lemmában szereplő a)-c) tulajdonságok teljesülnek és
$$f(a)\cdot f(b)\neq 0$$
(Könnyen belátható, hogy az előzőekben bemutatott maradékképző eljárással kapott elemekre a Lemmában megadott tulajdonságok teljesülnek).
A (6.29) $x$ helyen vett helyettesítési értékeinek sorozatában a jelváltások számát jelöljük $S(x)$-szel (nem vesszük figyelembe a sorozat nulla értékeit).
6.3. Tétel (Sturm-tétel (1842)).
Legyen
$$f_0(x), f_1 (x), …, f_m (x)$$
Sturm-sorozat. Akkor a $f(x)=0$ egyenletnek az $(a, b)$ intervallumon $S(b)-S(a)$ számú valós gyöke van.
A bizonyítás egyszerűen elvégezhető. Amíg az x értékek sorozata végigfut az $[a, b]$ intervallumon, a felvett értékek három csoportba sorolhatók:
1) $x$ nem gyöke a Sturm sorozat egyetlen tagjának sem. Ekkor a helyettesítési értékek előjele változatlan.
2) $x$ gyöke valamelyik közbülső polinomnak. A Lemma b) tulajdonsága alapján belátható, hogy a jelváltások eltolódnak, tehát a számuk nem változik.
3) $x$ gyöke az eredeti polinomnak, ekkor az áthaladás során az előjelváltások száma pontosan eggyel csökken.
6.6. Példa
$$g(x)=x^5+2x^4-5x^3+8x^2-7x-3=0$$
Maxima-ban:
wxplot2d(x^5+2*x^4-5*x^3+8*x^2-7*x-3,[x,-4,2],[style,[lines,6,2]],[axes, solid], [gnuplot_preamble, "set term pngcairo font 'Arial,16';"]),wxplot_size=[1024,768];

A Newton-tétel alapján
$$g(x)=x^5+2x^4-5x^3+8x^2-7x-3$$
$$g′(x)=5x^4+8x^3-15x^2+16x-7,$$
$$g′′(x)=20x^3+24x^2-30x+16,$$
$$g′′′(x)=60x^2+48x-30,$$
$$g^{(4)}(x)=120x+48$$
$$g^{(5)}(x)=120$$
Mivel
$$g(2)>0, g′(2)>0, g′′(2)>0, g′′′(2)>0, g^{(4)}(2)>0, g^{(5)}(2)>0,$$
a pozitív gyökkorlát $N<2$.
A negatív gyökkorlátot $N_2$-t a
$$g_2 (x)= -g(-x)$$
segéd-polinom alapján határozzuk meg:
$$g_2(x)=x^5-2x^4-5x^3-8x^2-7x +3$$
$$g′_2(x)=5x^4-8x^3-15x^2-16x-7$$
$$g′′_2(x)=20x^3-24x^2-30x-16$$
$$g′′′_2(x)=60x^2-48x-30$$
$$g(4)_2(x)=120x-48$$
$$g(5)_2(x)=120$$
Mivel
$$g_2(4)>0, g′_2(4)>0, g′′_2(4)>0, g′′′_2(4)>0, g^{(4)}_2(4)>0, g^{(5)}_2(4)>0$$
akkor a negatív gyökök $>-4$.
A Sturm-tétel alkalmazása:
$$g(x)=x^5-2x^4-5x^3-8x^2-7x+3$$
$$g_1(x)=5x^4+8x^3-15x^2+16x-7$$
$$g_2(x)=66x^3-150x^2+172x +61$$
$$g_3(x)=-464x2+1135x +723$$
$$g_4(x)=-32599457x -8486093$$
$$g_5(x)=-1$$
| $x$ | $g(x)$ | $g_1(x)$ | $g_2(x)$ | $g_3(x)$ | $g_4(x) $ | $g_5(x)$ | $S(x)$ |
|---|---|---|---|---|---|---|---|
| –∞ | – | + | - | - | + | - | 4 |
| ∞ | + | + | + | - | - | - | 1 |
Ez alapján: $(S(–∞)-S(∞)) =3$, és a $g(x)=0$ egyenletnek 3 valós gyöke van.
Megjegyzés: Az $S(–4)-S(2)$ meghatározása ugyanezt az eredményt adja.
Javasoljuk megoldani a 10. Fejezetben található feladatokat.
6.3. Lobacsevszkij-féle módszer
Elemezzük a
$$a_0 x^n + a_1 x^{n-1} + a_2 x^{n-2} + … + a_{n-1} x+ a_n=0 \tag{6.30}\label{eq:6.30}$$ (6.30)
algebrai egyenletet, vagy átalakítás után:
$$x^n + a_1 x^{n-1} + a_2 x_{n-2} + … + a_{n-1} x+ a_n=0 \tag{6.31}\label{eq:6.31}$$ (6.31)
Ha $\{x_1,x_2,...,x_n\}$ – a $\eqref{eq:6.31}$ (6.31) gyökei, akkor a Viett-tétel alapján a következő egyenletrendszert szerkeszthetünk:
$$\begin{equation}\begin{aligned} x_1+x_2+\ldots+x_n &= -a_1\\ x_1x_2+ x_1x_3 \ldots x_{n-1}x_n &= a_2\\ x_1x_2x_3 + x_1x_2x_4 + \ldots +x_{n-2} x_{n-1}x_n &= -a_3 \\ \cdots\cdots\cdots & \cdots \\ x_1x_2x_3 …x_n &= (–1)^na_n \end{aligned}\end{equation}\tag{6.32}\label{eq:6.32}$$ (6.32) Feltételezzük, hogy: $$|x_1| \gg |x_2| \gg … \gg |x_n|\tag{6.33}\label{eq:6.33}$$ (6.33) Akkor $$x_1 \left( 1 + \frac{x_2}{x_1} + \frac{x_3}{x_1} + \ldots + \frac{x_n}{x_1} \right) = -a_1 \tag{6.34}\label{eq:6.34}$$ (6.34) $$x_1 ≈ -a_1 \tag{6.35}\label{eq:6.35}$$ (6.35) $$x_1x_2 \left[1 + \frac{x_1x_3}{x_1x_2} +… + \frac{x_{n-1}x_n}{x_1x_2}\right] = a_2 \tag{6.36}\label{eq:6.36}$$ (6.36) $$x_1 x_2 ≈ a_1 \tag{6.37}\label{eq:6.37}$$ (6.37) $$x_2 ≈ -\frac{a_2}{a_1}\tag{6.38}\label{eq:6.38}$$ (6.38) $$x_i ≈ -\frac{a_i}{a_{i-1}},\quad i=1,…,n \tag{6.39}\label{eq:6.39}$$ (6.39) az $a_0=1$.
Ahhoz, hogy növeljük a gyökök közti távolságot, és egyben igaz legyen a (6.33), egyszer vagy többször végre kell hajtani a kvadratálási eljárást, amelyet a következő képen lehet végrehajtani:
Mivel ${x_1,x_2,...,x_n}$ – a polinom gyökei, akkor
$$a_0(x - x_1) (x - x_2) …(x - x_n) =0 \tag{6.30a}\label{eq:6.30a}$$ (6.30a)
és a
$$a_0(x + x_1) (x + x_2) …(x + x_n) =0 \tag{6.31a}\label{eq:6.31a}$$ (6.31a)
egyenlet gyökei pedig $\{-x_1, -x_2,..., -x_n\}$ lesznek.
A (6.30a),(6.31a) szorzata:
$$a^2_0(x^2-x_1^2)(x^2-x_2^2) …(x^2-x_n^2) =0 \tag{6.32a}\label{eq:6.32a}$$ (6.32)
lesz. Ha új változókat bevezetünk:
$$z= -x^2\tag{6.33a}\label{eq:6.33a}$$ (6.33)
akkor
$$a_0^2 (-z-x_1^2) (-z-x_2^2) …(-z-x_n^2) =0\tag{6.34a}\label{eq:6.34a}$$ (6.34a)
és a (6.34a) gyökei:
$$(-x_1^2,-x_2^2, …,-x_n^2)\tag{6.35a}\label{eq:6.35a}$$ (6.35a)
lesznek.
A (6.30a), (6.31a) szorzatnak egy másik alakja:
$$a_0^2x^{2n} + (a_1^2-2 a_0 a_2) x^{2n-2}+ (a_2^2-2 a_1 a_2+2 a_0 a_4) x^{2n-4}-….+(–1)^n a_n^2=0\tag{6.36a}\label{eq:6.36a}$$ (6.36a)
mivel $z=-x^2$, akkor átalakíthatjuk a (6.36a):
$$a_0^2z^n + (a_1^2-2a_0 a_2) z^{n-1}+ (a_2^2-2 a_1 a_2+2 a_0 a_4) z^{n-2}-….+(–1)^n a_n^2=0 \tag{6.37a}\label{eq:6.37a}$$ (6.37a)
vagy
$$b_0z^n + b_1z^{n-1}+ b_2 z^{n-2}–….+b_n=0 \tag{6.38a}\label{eq:6.38a}$$ (6.38a)
ahol
$$b_k=a_k^2-2 a_{k-1} a_{k+1}+2 a_{k-2} a_{k+2}-2 a_{k-3} a_{k+3}+2 a_{k-4} a_{k+4} \tag{6.39a}\label{eq:6.39a}$$ (6.39a)
A $b_k$ együtthatókat csak addig lehet szerkeszteni a (6.39a) alapján, amíg nem érjük el az $a_0$ vagy az $a_n$ tagokat.
A $\eqlabel{eq:6.30a}$ (6.30a) – (6.39a) képletek végrehajtása egy kvadratálási lépésnek felelnek meg. Szükség esetén a kvadratálást lehet tovább folytatni. Ha a gyökök közötti távolságokra fennáll a (6.33a) feltétel, akkor az utolsó egyenletre alkalmazhatjuk a Lobacsevszkij-féle módszert, és utána visszatérünk az eredeti $x$ változóhoz.
6.7. Példa
$$x^3-6x^2+11x-6=0$$
$$x_1=1,\quad x_2=2,\quad x_3=3$$
$$(x–1)(x–2)(x–3)=0$$
$$x^3+6x^2+11x+6=0$$
$$(x+1)(x+2)(x+3)=0$$
$$x_1=–1,\quad x_2=-2,\quad x_3=-3 $$
$$(x^2-1)(x^2-4)(x^2-9)=0$$
$$z= -x^2$$
$$x^6+(6x^5-6x^5)+ (11x^4-36x^4+11x^4)+ (6x^3-6x^3)+$$
$$(-36x^2+121x^2 -36x^2) +(66x-66x) -36=0$$
$$z^3-14z^2+49z-36=0$$
$$(z-1)(z-4)(z-9)=0$$
Az eredeti gyökökhöz képest $( -1, -2, -3)$ a kvadratálás a gyökök közti távolságot megnövelte: $(1, 4, 9)$.
6.4. Intervallumfelező eljárás
$$f(x)=0$$
Feltételezzük, hogy az $f(x)$ függvény az $[a, b]$ intervallumon folytonos és
$$f(a)f(b)<0\tag{6.40}\label{eq:6.40}$$ (6.40)
A Bolzano-tétel alapján a $(a, b)$ intervallumon a $f(x)=0$ egyenletnek legalább egy gyöke $x^*$ van. Kiszámítjuk a $(a, b) $ intervallum c felezőpontját:
$$c=\frac{a+b}{2}\tag{6.41}\label{eq:6.41}$$ (6.41)
Ha $f(x)=0$, akkor a $c$ pont az egyenlet gyöke;
ha $f(c)=0$, akkor a gyök keresését folytatjuk a $[a, c]$, vagy a $[c, b]$ intervallumban úgy, hogy
$$b=c,\text{ ha } f(a)f(c)<0,$$
vagy
$$a=c,\text{ ha }f(c)f(b)<0.$$
Akkor az új $[a, b]$ intervallumra is igaz a
$$f(a)f(b)<0$$
feltétel. Az $n$ számú lépés végrehajtása után az intervallum hossza:
$$b_n-a_n=\frac{b-a}{2^n}\tag{6.42}\label{eq:6.42}$$ (6.42)
és
$$b_n-a_n\xrightarrow[n\to\infty]{} 0\tag{6.43}\label{eq:6.43}$$ (6.43)
Az iterációs folyamatot akkor lehet befejezni, ha
$$|b-a|<δ, $$ (6.44)
vagy
$$|f(c)|<ɛ.$$ (6.45)
Az utóbbi egyenlőtlenség a függvény értékének a pontosságát mutatja, és nem a gyökét.
A $δ$ (vagy $ɛ$) a megoldás pontosságát határozzák meg. Mivel végtelen számú lépést nem hajthatunk végre, az iterációt bizonyos $n$ értéknél meg kell szakítani.
Javasoljuk megoldani a 10. Fejezetben található feladatokat.
6.5 Húrmódszer
$$f(x)=0$$
Ha a $f(x)$ függvény folytonos, és $f(a)f(b)<0$, akkor az $(a, f(a))$ és a $(b, f(b))$ pontokon keresztül egy húrt (szakaszt) szerkesztünk, amelynek az egyenletét a két ponton átmenő egyenes egyenletéből kaphatjuk meg:
$$y-y_1=(x-x_1) \frac{y_2-y_1}{x_2-x_1};$$
Legyen
$$x_1=a;\quad x_2=b;\quad y_1=f(a);\quad y_2=f(b) $$
A helyettesítés, illetve a rendezés végrehajtása után a következő egyenletet kapjuk:
$$\frac{x-a}{b-a}=\frac{y-f(a)}{f(b)-f(a)}\tag{6.46}\label{eq:6.46}$$ (6.46)
Legyen a $c$ pont a húr és az $x$ tengely olyan metszéspontja, ahol $y=0$. Akkor:
$$\frac{c-a}{b-a}=-\frac{f(a)}{f(b)-f(a)}$$
$$\frac{c-a}{f(b) -f(a)}= -f(a) (b-a)$$
$$c=\frac{af(a)-bf(a)}{f(b)-f(a)}+a \tag{6.47}\label{eq:6.47}$$ (6.47)
vagy
$$c= \frac{af(b) -bf(a)}{f(b) -f(a)}$$ (6.48)
Ha $f(c)=0$, akkor a $c$ pont az egyenlet gyöke,
ha $f(c)≠0$, akkor a gyök keresését folytathatjuk az $[a,c]$, vagy a $[c,b]$ intervallumban.
Ha $f(a)f(c)<0$, akkor $b=c$,
ha $f(c)f(b)<0$, akkor $a=c$.
Az iterációs folyamat akkor fejeződik be, ha
$$|b-a|<δ\tag{6.49}\label{eq:6.49}$$ (6.49)
Javasoljuk megoldani a 10. Fejezetben található feladatokat.
6.6 Newton-Raphson (érintő) módszer
Feltételezzük, hogy létezik $f′(x)$. Eben a módszerben a gyök közelítése az érintő mentén történik. Az $x_0$ pontban az érintő képletét az adott ponton átmenő, adott meredekségű egyenes egyenletéből kapjuk meg:
$$y-y_1=m(x-x_1);\quad x_1 =x_0;\quad y_1=f(x_0), m=f′(x_0)$$
$$y-f(x_0)=f′(x_0)(x-x_0)\tag{6.50}\label{eq:6.50}$$ (6.50)
A (6.50) egyenletből megtalálhatjuk az érintő és az $x$ tengely metszéspontját, ahol $y=0$
$$–f(x_0)=f′(x_0)(x-x_0),$$
$$x-x_0 = - \frac{f(x_0)}{f′(x_0)}$$
$$x_1=x_0 - \frac{f(x_0)}{f′(x_0)},$$
$$x_{n+1}=x_n - \frac{f(x_n)}{f′(x_n)}\quad n=0,1,2,... \tag{6.51}\label{eq:6.51}$$ (6.51)
A Newton-Raphson módszer hiba-becslése.
Legyen $x^*$ az egyenlet gyöke. Akkor
$$0=f(x^*)=f(x_n)+f′(x_n)(x^*-x_n)+f′′(ξ)\frac{(x^*-x_n)^2}{2} \tag{6.52}\label{eq:6.52}$$ (6.52)
és
$$\frac{f(x_n)}{f′(x_n)}=x_n-x^*-f′′(ξ)\frac{(x^*-x_n)^2}{2f′(x_n)} \tag{6.53}\label{eq:6.53}$$ (6.53)
Innen
$$x_{n+1} - x^* = x_n–x^*-\frac{f(x_n)}{f′(x_n)} = (x^*-x_n)^2 \frac{f′′(ξ)}{2f′(x_n)} \tag{6.54}\label{eq:6.54}$$ (6.54)
Ha
$$m_1=\min|f′(x)|, \quad M_2=\max|f′′(x)|, $$
jelöléseket alkalmazzuk, akkor megkapjuk a hiba-becslés képletét:
$$|x_{n+1} - x^*| \leqslant |x_n – x^*|^2 M_2/(2m_1) \tag{6.55}\label{eq:6.55}$$ (6.55)
A (6.51) iterációs folyamat (tetszőleges kezdőpontból kiindulva) akkor konvergens, ha teljesül a következő feltétel:
$$|f(x)\cdot f′′(x)|<f′(x)^2\tag{6.56}\label{eq:6.56}$$ (6.56)
4. Tétel (konvergencia elégséges feltétele).
Ha $f(a)f(b)<0,$ az $f′(x)$ és $f′′(x)$ függvények előjele az $[a,b]$-n nem változik, és
$$f(x_0)f′′(x_0)>0, \tag{6.57}\label{eq:6.57}$$ (6.57)
$$x_0\in[a,b],$$
akkor a (6.51) iterációs folyamat konvergens.
Az érintő módszer nem alkalmazható, ha $f′(x)=0$, vagy $|f′(x)|<ɛ$. Ha az $f(x)=0$ egyenletnek nincs gyöke, akkor az $f′(x_n)$ előjele iterációnként változik.
Javasoljuk megoldani a 10. Fejezetben található feladatokat.
6.7 Szelőmódszer
Ha nem tudjuk vagy nem akarjuk a (6.51) képletben a függvény deriváltját alkalmazni, akkor azt az osztott differenciával lehet közelíteni:
$$g(x_n)=\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}, \tag{6.58}\label{eq:6.58}$$ (6.58)
$$x_{n+1}=x_n-\frac{f(x_n)}{g(x_n)},\quad n=0, 1, 2,... \tag{6.59}\label{eq:6.59}$$ (6.59)
Ha a $g(x_n)$-t be helyettesijük a (6.59)-be, akkor
$$x_{n+1}=x_n-\frac{f(x_n)}{\displaystyle\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}}=x_n-f(x_n)\frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})} \tag{6.60}\label{eq:6.60}$$ (6.60)
és a következő iterációs képletet kapjuk:
$$x_{n+1}=\frac{f(x_n)x_{n-1}-f(x_{n-1})x_n} {f(x_n)-f(x_{n-1})}, \quad n=0, 1, 2,.. \tag{6.61}\label{eq:6.61}$$ (6.61)
Az iterációs folyamat elindítására két kezdő pontra $x_0$ és $x_1$ van szükség.
6.8 Érintő és a húrmódszer közös alkalmazása
a) Ha teljesül a
$$f(a)⋅f′′(a)>0\tag{6.62}\label{eq:6.62}$$ (6.62)
feltétel, akkor az iterációs folyamatot így lehet elindítani:
$$x_0=a –\frac{f(a)}{f′(a)},\quad x_1=\frac{af(b)-bf(a)}{f(b)-f(a)} \tag{6.63}\label{eq:6.63}$$ (6.63)
b) Ha
$$f(a)f′′(a)>0\tag{6.64}\label{eq:6.64}$$ (6.64)
akkor pedig:
$$x_0=b -\frac{f(b)}{f′(b)},\quad x_1=\frac{af(b)-bf(a)}{f(b)-f(a)} \tag{6.65}\label{eq:6.65}$$ (6.65)
Az iterációk folytatása a következő képletek szerint történik:
$$x_{2n} = x_{2n-2} - \frac{f(x_{2n-2})}{f′(x_{2n-2})} \tag{6.66}\label{eq:6.66}$$ (6.66)
$$x_{2n+1}=\frac{x_{2n-2}f(x_{2n-1}) - x_{2n-1}f(x_{2n-2})} {f(x_{2n-1}) - f(x_{2n-2})} \tag{6.67}\label{eq:6.67}$$ (6.67)
6.9 Fixpont iterációs módszer (Fokozatos közelítés módszere)
Átalakítjuk az $f(x)=0$ egyenletet
$$x=g(x) \tag{6.68}\label{eq:6.68}$$ (6.68)
Az mondjuk, hogy $x^*$ a $g(x)$ függvény fixpontja, ha $x^*= g(x^*)$.
6.5. Tétel
Ha $g\in\mathbb{C}[a,b]$ és $a\leqslant g(x)\leqslant b$ minden $x\in[a,b]$ esetén, akkor a $g(x)$ függvénynek az $[a,b]$ intervallumon van fixpontja.
Definíció.
A $g\in\mathbb{C}[a,b]$ függvény kontrakció az $[a,b]$ intervallumon, ha létezik olyan
$$0\leqslant q<1,\tag{6.69}\label{eq:6.69}$$ (6.69)
hogy
$$|g(x)-g(y)| \leqslant q |x-y|,$$
$x,y\in[a,b]$.
6.8. Példa
A $g(x)=x^2$ függvény kontrakció a $\left[0,\displaystyle\frac{1}{4}\right]$ intervallumon, mivel
$$|x^3-y^2|= |x+y|\, |x-y| \leqslant\frac{|x-y|}{2},$$
ha
$$x, y\in\left[0, \frac{1}{4}\right].$$
6.6. Tétel
Ha $(x\in[a,b])$, $a\leqslant g(x)\leqslant b$, és $g(x)$ kontrakció $[a,b]$-n, akkor pontosan egy fixpont létezik az $[a,b]$ intervallumon.
6.7. Tétel
A $g\in\mathbb{C}^1[a,b]$ függvény kontrakció az $[a,b]$-n, ha
$$\max_{x\in[a,b]}|g^\prime(x)|=q<1.\tag{6.70}\label{eq:6.70}$$ (6.70)
6.8. Tétel
Legyen $g\in\mathbb{C}[a,b]$ olyan, hogy
$$a\leqslant g(x)\leqslant b\quad (x\in[a,b]) \tag{6.71}\label{eq:6.71}$$ MATH (6.71)
és $g(x)$ kontrakció az $[a,b]$ -n.
Ekkor minden $x_0\in[a,b]$ esetén az
$$x_{n+1}=g(x_n),\quad n=0, 1, 2, … \tag{6.72}\label{eq:6.72}$$ (6.72)
iterációs sorozat lineáris sebességgel konvergál az $x^*$ fixponthoz, azaz
$$|x_i - x^*|\leqslant q_i|x_0 - x^*|,\quad i=0, 1, 2, ...\tag{6.73}\label{eq:6.73}$$ (6.73)
A $x=g(x)$ egyenlet fixpont iterációs eljárása:
Az $x_0$ kezdő pont kiválasztása után végrehajtjuk az iterációs folyamatot:
$$x_{n+1}=g(x_n),\quad n=0, 1, 2, … \tag{6.74}\label{eq:6.74}$$ (6.74)
Ha a sorozat konvergens, akkor
$$x^* =g(x^*) \tag{6.75}\label{eq:6.75}$$ (6.75)
vagy is
$$f(x^*) =0$$
A konvergencia elégséges feltétele:
$$|g′(x)|<q<1$$
a következő tétel alapján.
6.9. Tétel
Ha $g\in\mathbb{C}[a,b]$ differenciálható és
$$a\leqslant g(x)\leqslant b\quad (x\in[a,b]),$$
és létezik olyan $q$, hogy
$$|g′(x)|\leqslant q<1 \tag{6.76}\label{eq:6.76}$$ (6.76)
akkor minden $x_0\in[a,b]$ esetén a
$$x_{n+1}=g(x_n),\quad n=0, 1, 2, … $$
iterációs sorozat konvergál az $x^*$ fixponthoz.
6.9. Példa
Oldjuk meg a fokozatos közelítési módszerrel az
$$e^x-10x=0$$
egyenletet $ɛ=0,\!0001$ pontossággal.
Átalakítjuk az egyenletet
$$e^x =10x$$
és grafikus módszerrel a Maxima segítségével megállapítjuk azokat az intervallumokat, ahol a gyököket keresni érdemes.
wxplot2d([exp(x),10*x],[x,-0.2,3.8],[style,[lines,6,2],[lines,6,3]],[axes, solid],[legend, "e^x", "10x"], [gnuplot_preamble, "set term pngcairo font 'Arial,16';"]),wxplot_size=[1024,768];
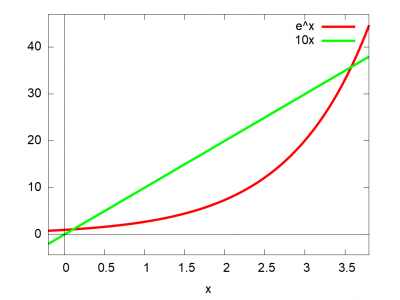
Az egyenletnek két gyöke van: $x^*_1\in[0,1],\,\, x^*_2\in[2,6]$.
Az első gyök keresésére az egyenletet átalakítjuk
$$x=g(x)=0,\!1 e^x$$
A $[0,1]$ intervallumon:
$$g′(x) = 0,\!1 e^x$$
$$0\leqslant g′(x) \leqslant 1,$$
Akkor
$$q<0,\!1.$$
Kiválasztjuk a $x_0=1$, és a fokozatos közelítési módszer alapján a következő iterációkat kapunk:
$$x_1 = 0,\!271828$$
$$x_2 =0,\!131236$$
$$x_3=0,\!114024$$
$$x_4=0,\!112078$$
$$x_5=0,\!111860$$
$$x_6=0,\!111835$$
Mivel
$$|x^*_1-x_6| \leqslant 0,\!1\frac{|x_5-x_6|}{1-0,\!1} \leqslant \frac{0,\!00004}{9} \leqslant 0,\!000005,$$
$$x^*_1 ≈ 0,\!11183$$
Az eredmény összes számjegye biztos.
A második gyök keresésére az egyenletet így kell átalakítani:
$$x=g(x)=\ln(10x).$$
$$g′(x)=\frac{1}{x}$$
Akkor a [2,6] intervallumon:
$$|g′(x)| = \left|\frac{1}{x}\right| \leqslant 0,\!5$$
és
$$q<0,\!5.$$
Legyen $x_0=2$ akkor a fokozatos közelítési módszer alapján megkapjuk a gyök következő közelítéseit:
$$x_1=2,\!99573$$
$$x_2=3,\!39977$$
$$x_3=3,\!52629$$
$$x_4=3,\!56283$$
$$x_5=3,\!57314$$
$$x_6=3,\!57603$$
$$x_7=3,\!57684$$
$$x_8=3,\!57706$$
$$x_9=3,\!57713$$
Mivel
$$|x^*_2-x_9| \leqslant 0,\!5\frac{|x_8 - x_9|}{1-0,\!5} \leqslant 0,\!0001$$
$$x^*_2 ≈ 3,\!5771$$
és az eredmény összes számjegye biztos.
Javasoljuk megoldani a 10. Fejezetben található feladatokat.

