II. RF KMF DokuWiki

A polinomok

$$p(x) = a_0 x^n+ a_1 x^{n-1}+\ldots +a_{n-1} x + a_n\tag{2.1}\label{eq:2.1}$$

alkotják a függvények legegyszerűbb osztályát, és a következő formula alapján könnyen kiértékelhetők.

Horner-féle elrendezés

(Horner W. (1786-1837) - angol matematikus).

Átalakítjuk a $\eqref{eq:2.1}$ képletet

$$p(x) = (a_0 x^{n-1}+ a_1 x^{n-2}+\ldots+ a_{n-1})\, x + a_n = \\ = \left(\,(a_0 x^{n-2}+ a_1 x^{n-3}+\ldots + a_{n-2})\, x + a_{n-1}\right)\,x + a_n=\ldots = \\ = \left(\ldots (a_0 x+ a_1) x+ \ldots+ a_{n-2}\right)\, x + a_{n-1})\,x + a_n \tag{2.2}\label{eq:2.2}$$

Akkor a $\eqref{eq:2.2}$ alapján a $p(x)$ kiértékelése a következő algoritmus szerint történik:

$$s=a_0, \\ s=s·x+a_1, \\ s=s·x+a_2, \\ \cdots\\ s=s·x+a_n,\tag{2.3}$$

ami egy ciklusban könnyen kiszámítható:

$$s=a_0, \\ s=s·x+a_k,\quad k=1, 2, \ldots, n. \tag{2.4}\label{eq:2.4}$$

A $\eqref{eq:2.4}$ algoritmusnak az előnye, hogy a polinom kiértékelésére csak $n$ szorzás szükséges.

2.1. Példa

Számítsuk ki a

$$p(x) =x^7 - 2x^6+ x^5 - 3x^4+4x^3 - x^2+6x - 1$$

értékét a $-1,\!5$ pontban!

$$p(-1,\!5)= -88,\!3985.$$

Mint ismeretes, a matematikai műveletek közül a számítógépek csak a négy alapvető aritmetikai műveletet képesek végrehajtani. Ezért a transzcendens függvényeket csak numerikus módszerekkel lehet kiértékelni. Ezek a módszerek azon az elven alapszanak, hogy a $f(x)$ transzcendens függvényt egy olyan $p(x)$ függvénnyel (leggyakrabban polinommal)

$$f(x)≈ p(x)\tag{2.5}$$

közelítjük, melynek a kiértékelése nem okoz problémát. A közelítések gyakran a deriváltok alkalmazásával történnek, mivel azok fontos információt tartalmaznak a függvényről. Mivel

$$f^\prime(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h},\tag{2.6}$$

vagy $$\frac{f(x+h)-f(x)}{h}=f^\prime(x)+a(h),$$

$$\lim_{h\rightarrow 0}a(h)=0,$$

akkor

$$f(x+h)\approx f(x) +h f^\prime(x)$$

vagy egy másik alakban:

$$f(x)\approx f(x_0) + f^\prime( x_0)(x-x_0). \tag{2.7}\label{eq:2.7} $$

Ha a $f(x_0)$ és $f^\prime(x_0)$ értékeit könnyen tudjuk kiszámítani, akkor a $\eqref{eq:2.7}$ alapján kiszámíthatjuk az $f(x)$ függvényt értékét.

Például, legyen $f(x)=x^a$, $x_0=1$. Akkor $f(1)=1$,

$$f^\prime(x) =ax^{a-1},\quad f^\prime(x) =a$$.

Ha $x=1+\Delta$, akkor $(1+\Delta)a\approx 1+a\Delta. $

2.2. Példa

$$\sqrt[7]{1,\!07}=(1+0,\!07)^{\frac{1}{7}}\approx 1+\frac{1}{7}0,\!07=1,\!01. $$

Taylor-sor alkalmazása

Ha a függvény magasabb rendű deriváltjai is léteznek, akkor szerkeszthetünk Taylor-sort

$$f(x)=f(x_0)+f^\prime(x_0)(x-x_0)+\frac{f^{\prime\prime}(x_0)}{2!}(x-x_0)^2+\ldots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+\ldots\tag{2.8}\label{eq:2.8}$$

a Taylor-formulát maradéktaggal így írhatjuk le:

$$f(x)=f(x_0)+f^\prime(x_0)(x-x_0)+\frac{f^{\prime\prime}(x_0)}{2!}(x-x_0)^2+\ldots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x),\tag{2.9}\label{eq:2.9}$$

ahol

$$R_n(x)=\frac{f^{(n+1)}\left(x_0+\zeta(x-x_0)\right)}{(n+1)!}(x-x_0)^n\tag{2.10}\label{eq:2.10}$$

$$0< ζ(x,n)<1$$

a Lagrange-féle maradéktag.

Mivel a Taylor-sor összegzésének az eredménye nem mindig egyenlő a $f(x)$ függvény értékével, minden konkrét esetben ellenőrizni kell azt, hogy

$$\lim_{n\to\infty}R_n(x)=0\tag{2.11}\label{eq:2.11}$$

Maclaurin-formula

A Taylor-formulából $x_0=0$ esetén Maclaurin-formulát kapunk:

$$f(x)=\sum_{k=0}^n\frac{f^{(k)}(0)}{k!}(x)^k+R_n(x),\tag{2.12}\label{eq:2.12}$$ $$p(x)=\sum_{k=0}^n\frac{f^{(k)}(0)}{k!}x^k,\tag{2.13}\label{eq:2.13}$$

$$f(x)≈p(x).\tag{2.14}\label{eq:2.14}$$

A $\eqref{eq:2.12}-\eqref{eq:2.14}$ képletek alapján több elemi transzcendens függvényt lehet közelíteni. A közelítés hiba-becslését a

$$R_n(x)= |f(x)-P(x)|=\sum_{k={n+1}}^\infty\frac{f^{(k)}(0)}{k!}x^k\tag{2.15}\label{eq:2.15}$$

formula alapján lehet megadni.

Néhány konkrét függvény elemzése.

a) Exponenciális függvény

$$y=e^x$$

$$e^x=\sum_{k=0}^n\frac{x^k}{k!},\quad(-\infty<x<\infty)\tag{2.16}\label{eq:2.16}$$

$$e^x=\sum_{k=0}^n u_k,\quad u_k=\frac{x^k}{k!}\tag{2.17}\label{eq:2.17}$$

$$u_{k-1}=\frac{x^{k-1}}{(k-1)!},\quad u_k=\frac{x}{k}u_{k-1},\tag{2.18}\label{eq:2.18}$$

$$u_0=1, \quad S_0=1,\quad S_k=S_{k-1}+u_k\tag{2.19}\label{eq:2.19}$$

Ha $0<2|x|\leqslant n$, és $|x|\leqslant\displaystyle\frac{n}{2}$,

akkor

$$|R_n(x)|< |u_n|\tag{2.20}\label{eq:2.20}$$

Ezt az összegzést addig folytatjuk, amíg nem teljesül a

$$|u_n|<ε\tag{2.21}\label{eq:2.21}$$

feltétel.

Az összegzés iterációs algoritmussal történik, mely a $\eqref{eq:2.18},\eqref{eq:2.19}$ és $\eqref{eq:2.21}$ képleteken alapszik.

A $|x|$ értékének növekedésével a Maclaurin-formula maradéktagja is növekszik, és ezért nagy $|x|$ esetén ezt az algoritmust nem ajánlatos alkalmazni. Ha lehetőség van, akkor a függvények tulajdonsága alapján csökkenthetjük az $|x|$ értékét.

Például, a $e^x$ függvény esetén ez könnyen megoldható a következő felbontással:

$$x=E(x)+q, \quad 0\leqslant q<1,\tag{2.22}$$

$$e^x= e^{E(x)}\cdot e^q.\tag{2.23}$$

Mivel $0\leqslant q<1$, akkor a Maclaurin-sor gyorsan konvergál, és a hibabecslés értéke:

$$0\leqslant R_n(q)<\frac{q_{n+1}}{(n!·n)} \tag{2.24}$$

2.3. Példa

Számítsuk ki a $\sqrt{e}$ értékét $10^{-5}$ pontossággal!

$$\sqrt{e}= \sum_{k=0}^n u_k+R_n\left(\frac{1}{2}\right),$$

$$u_0=1,\quad u_k= \frac{u_{k-1}}{2k},\quad k=1, 2, \ldots, n$$

$$\begin{equation} \left.\begin{aligned} k \quad &u_k \\ 0 \quad &1 \\ 1 \quad &0,\!5 \\ 2 \quad &0,\!125 \\ 3 \quad &0,\!0208333 \\ 4 \quad &0,\!0026042 \\ 5 \quad &0,\!0002604 \\ 6 \quad &0,\!0000217 \\ 7 \quad &0,\!0000016 \\ S= &1,\!6487212 \end{aligned}\right. \end{equation}$$ Az eredmény: $\sqrt{e}=1,\!64872$.

b) Trigonometrikus függvények

$$y=\sin x$$

$$\sin x=\sum_{k=0}^\infty(-1)^k\frac{x^{2k+1}}{(2k+1)!},\quad(-\infty<x<\infty)\tag{2.25}\label{eq:2.25}$$ (2.25)

$$\sin x=\sum_{k=0}^n u_n+R_n(x)\tag{2.26}\label{eq:2.26}$$ (2.26)

$$u_1=x,\quad u_{k+1}= -x^2 \frac{u_k}{2k\cdot(2k+1)},\quad k=1, 2, \ldots, n-1.\tag{2.27}\label{eq:2.27}$$

$$s=x_1,\quad s=s+u_k\tag{2.28}$$

$$|u_n|<ε\tag{2.29}\label{eq:2.29}$$

$$|R_n(x)|\leqslant \frac{|x|^{2n+1}}{(2n+1)!} =|u_{n+1}|\tag{2.30}$$

Ebben az esetben az iterációs algoritmust a $\eqref{eq:2.27}-\eqref{eq:2.29}$ képletek alapján szerkesztjük.

$$y=\cos x$$

$$\cos x=\sum_{k=0}^\infty(-1)^k\frac{x^{2k}}{(2k)!},\quad(-\infty<x<\infty)\tag{2.31}\label{eq:2.31}$$ (2.31)

$$\cos x=\sum_{k=0}^n u_n+R_n(x)\tag{2.32}\label{eq:2.32}$$ (2.32)

$$u_1=1,\quad u_{k+1}= -x^2 \frac{u_k}{(2k-1)\cdot 2k} \tag{2.33}\label{eq:2.33}$$

$$k=1, 2, …, n-1$$

Mivel a $\sin x$ és a $\cos x$ függvények periodikusak, ezért ezeket a képleteket elegendő csak az $x\in\left[0;\displaystyle\frac{\pi}{4}\right]$ intervallumon alkalmazni. Az elérhető pontosság szempontjából ez a lehetőség lényeges, mivel az $x$ növekedésével gyorsan növekszik a hiba-becslés értéke is.

2.4. Példa

Számítsuk ki a $\sin 23^\circ 54^\prime$ értékét, $ε=10^{-4}$, $x=0,\!41714$ radián.

$$ \left.\begin{aligned} &u_1=x=0,\!41714 \\ &u_2=-x^2\frac{u_1}{2·3}= -0,\!01210 \\ &u_3=x^2\frac{u_2}{4·5}= 0,\!00011 \\ &u_4=-x^2\frac{u_3}{6·7}= -0,\!0000 \\ &\sin 23^\circ 54^\prime=0,\!40515 \end{aligned}\right. $$

c) Hiperbolikus függvények

Hiperbolikus szinusz

$$y=\operatorname{sh} x=\frac{e^x- e^{-x}}{2},\quad y=\operatorname{ch} x=\frac{e^x+ e^{-x}}{2};\tag{2.34}$$

$$\operatorname{sh} x=\sum_{k=0}^\infty\frac{x^{2k-1}}{(2k-1)!},\quad(-\infty<x<\infty)\tag{2.35}\label{eq:2.35}$$ (2.35)

$$\operatorname{sh} x=\sum_{k=0}^n u_n+R_n(x) \tag{2.36}\label{eq:2.36}$$ (2.36)

$$u_1=x,\quad u_{k+1}=\frac{x^2}{2k\cdot(2k+1)}u_k,\quad k=1, 2, \ldots, n-1. \tag{2.37}\label{eq:2.37}$$ (2.37)

ha $n\geqslant |x|$, akkor

$$R_n< \displaystyle\frac{|u_n|}{3}.\tag{2.38}\label{eq:2.38}$$

Hiperbolikus koszinusz

$$\operatorname{ch} x=\sum_{k=0}^\infty\frac{x^{2k}}{(2k)!},\quad(-\infty < x < \infty) \tag{2.39}\label{eq:2.39}$$ (2.39)

$$\operatorname{ch} x=\sum_{k=0}^n u_n+R_n(x) \tag{2.40}\label{eq:2.40}$$ (2.40)

$$u_1=x,\quad u_{k+1}=\frac{x^2}{2k\cdot(2k-1)}u_k,\quad k=1, 2, \ldots, n-1. \tag{2.41}\label{eq:2.41}$$ (2.41)

ha $n\geqslant |x|$, akkor

$$R_n< 2\displaystyle\frac{|u_n|}{3}.\tag{2.42}$$

d) Logaritmikus függvény

Levezetjük a

$$y=\ln x$$

függvény Taylor-sorát.

Mivel

$$\frac{1}{1+t}=1-t+t^2-t^3+\ldots+(-1)^{n-1}t^{n-1}+ \frac{(-1)^nt^n}{1+t}, \tag{2.43}\label{eq:2.43}$$ (2.43)

és

$$\int\limits_0^x\displaystyle\frac{1}{1+t}\,dt =\left.\ln(1+t)\right|_0^n=\ln(1+x), \tag{2.44}\label{eq:2.44}$$ (2.44)

akkor

$$\ln(1+x)=\int\limits_0^x\displaystyle\frac{1}{1+t}\,dt= \int\limits_0^x\left[1-t+t^2-t^3+\ldots+(-1)^{n-1}t^{n-1}+ \frac{(-1)^nt^n}{1+t}\right]\,dt=$$

$$=x-\frac{x^2}{2}+\frac{x^3}{3}-\ldots+(-1)^{n-1}\frac{x^n}{n} +R_n(x)\tag{2.45}\label{eq:2.45}$$ (2.45)

$$R_n(x)=(-1)^{n}\int\limits_0^x\frac{t^n}{1+t}\,dt \tag{2.46}\label{eq:2.46}$$ (2.46)

A Taylor-sor a $x=1$ és $x=-1$ pontokban:

$$\ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\ldots +(-1)^{n-1}\frac{x^n}{n}+\ldots \tag{2.47}\label{eq:2.47}$$ (2.47)

$$\ln(1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-\ldots-\frac{x^n}{n}-\ldots \tag{2.48}\label{eq:2.48}$$ (2.48)

konvergens, ha $|x|\leqslant 1$

A wxMaxima alkalmazásával elemezzük a Taylor-sort a $\sin(x)$ függvény esetén.

Adjuk meg az $n$ értékét, azaz hogy hányadik kitevőig szeretnénk elvégezni a Taylor-sorba fejtést:

n:8;

8

taylor(sin(x), x, 0, n);

$x-\displaystyle\frac{x^3}{6}+\displaystyle\frac{x^5}{120}-\displaystyle\frac{x^7}{5040}+\ldots$

Átalakítjuk az eredményt polinommá:

define(p(x), ratdisrep(taylor(sin(x), x, 0, n)));

$x-\displaystyle\frac{x^3}{6}+\displaystyle\frac{x^5}{120}-\displaystyle\frac{x^7}{5040}+\ldots$

vagy

float(p(x));

$-1.984126984126984\,10^{-4}x^7+0.008333333333333333\,x^5-0.1666666666666667x^3+x$

Kiértékeljük a polinomot az $x=2$ pontban:

p(2.0);

$0.9079365079365079$

Ellenőrizzük az eredményt:

sin(2.0);

$0.9092974268256817$

A két érték eléggé közel van egymáshoz.

Értékeljük ki a $p(x)$ polinomot néhány további pontban is.

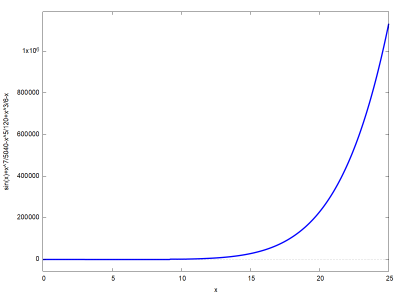
float(makelist(p(x), x, [2.0, 4.0, 10.0, 25.0]));

$ [0.9079365079365079,-1.384126984126984,-1307.460317460317,-1132213.963293651]$

A második eredmény már egyáltalán nem jó! A legutolsó meg, – fantasztikusan rossz!!!

Vizsgáljuk megy a pontos és a közelítő értékek közötti különbségeket:

float(makelist(sin(x) - p(x), x, [2.0, 4.0, 10.0, 25.0]));

$[0.001360918889173779,0.6273244888190554,1306.916296349428,1132213.830941901]$

Látható, hogy a $p(x)$ közelítés értékei egyre távolodnak a $\sin x$ pontos értékétől, mivel a különbségek egyre csak növekszenek.

Grafikonon ábrázolva ezt még szembetűnőbbé válik a különbség:

wxplot2d(sin(x) - p(x), [x, 0, 25], [style,[lines, 4]]);

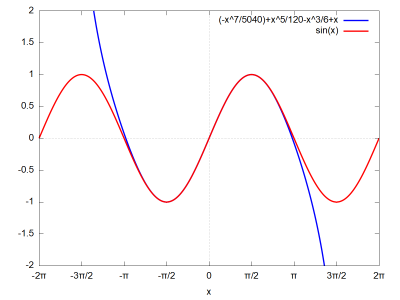
Ábrázoljuk egy grafikonon a két függvényt:

wxplot2d([p(x), sin(x)], [x, 0, 2*%pi], [style, [lines, 4]]);

Mint láthatjuk, ha $x>π$, akkor növekszik az eltérés.

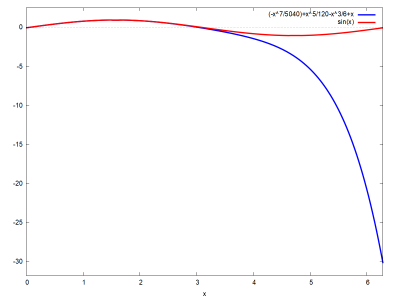
grafikonbeallitasok: "set xtics ('-2π' -6.283, '-3π/2' -4.712, '-π' -3.1415, '-π/2' -1.5708, '0' 0, 'π/2' 1.5708, 'π' 3.1415,'3π/2' 4.712, '2π' 6.283); set term pngcairo font 'Arial,14';"$

wxplot2d([p(x), sin(x)],
     [x, -2*%pi, 2*%pi], [y, -2, 2], [axes, x],[style,[lines,4]],
     [gnuplot_preamble, grafikonbeallitasok]);

Ezekből a példákból megállapítható, hogy amikor az $x$ távolodik a $0$ ponttól (Maclaurin-sor esetén), akkor lényegesen növekszik az abszolút hiba. Ez a tény sok esetben korlátozza a Taylor-formula alkalmazását.

Sokkal jobb eredményeket lehet elérni, ha a függvényeket ortogonális polinomokkal közelítjük.

Az $f(x)\in \mathbb{C}[a,b]$ függvény legkisebb négyzetes közelítése esetén természetes a következő norma alkalmazása:

$$\|f\|=\left(\int\limits_a^b f^2(x)\omega(x)dx\right)^\frac{1}{2}\hspace{-6pt}, \tag{2.49}\label{eq:2.49}$$

ahol a $\omega(x)>0$ – súlyfüggvény.

Diszkrét probléma.

Amikor a függvény értékei csak bizonyos pontokban adottak, akkor a $\eqref{eq:2.49}$ norma helyet

$$\|f\|=\left(\sum_{k=1}^{m} f^2(x_k)\omega(x_k)\right)^\frac{1}{2}\hspace{-6pt}, \tag{2.50}\label{eq:2.50}$$

normát alkalmazunk, ahol

$$a\leqslant x_1< x_2< \ldots < x_m\leqslant b$$

2.1. Tétel

Adott $f(x)\in \mathbb{C}[a,b]$ és legyen

$$\{\phi_i(x)\}^n_{i=1}\subset \mathbb{C}[a,b]$$

lineárisan független függvény rendszer. Akkor létezik pontosan egy legjobban közelítő függvény

$$\Phi(x)= \sum_{k=1}^{n} q_k\phi_k, \tag{2.51}\label{eq:2.51}$$

amelyre igaz, hogy

$$ \left\|f-\sum_{k=1}^{n} q_k\phi_k\right\|\leqslant\left\|f-\sum_{k=1}^{n} r_k\phi_k\right\|, \tag{2.52}\label{eq:2.52} $$

Diszkrét probléma esetben hasonló tétel bizonyítható.

A legjobb approximációs (közelítési) probléma akkor van megoldva, ha megállapítottuk a $q_k$ együtthatókat a

$$ \left\|f-\sum_{k=1}^{n} r_k\phi_k\right\|^2=\min, \tag{2.53}\label{eq:2.53} $$

feltétel alapján. Ez azt jelenti, hogy kell meghatározni a

$$S(r_1,r_2,\ldots,r_n)=\int\limits_a^b\left[\left( f(x)-\sum_{k=1}^{n} r_k\phi_k\right)^2\!\!\omega(x)\right]^2\!\!\omega(x)dx \tag{2.54}\label{eq:2.54} $$

függvény egyetlen minimumát, és ami a következő

$$\frac{\partial S(r_1,r_2,\ldots,r_n)}{\partial r_i}=0\quad i=1,\ldots,n\tag{2.55}\label{eq:2.55} $$

egyenletrendszer megoldásának felel meg.

Akkor:

$$\frac{\partial S(r_1,r_2,\ldots,r_n)}{\partial r_i}=-2\int\limits_a^b\left(f(x)-\sum_{k=1}^{n} r_k\phi_k(x)\right)\phi_i(x)\omega(x)dx=0.\tag{2.56}\label{eq:2.56} $$ Innen

$$\sum_{k=1}^{n}r_k\int\limits_a^b \phi_k(x)\phi_i(x)\omega(x)dx=\int\limits_a^b f(x)\phi_i(x)\omega(x)dx,\quad i=1,\ldots,n. \tag{2.57}\label{eq:2.57} $$

Bevezetjük a skalár-szorzatot:

$$\left\langle f,g \right\rangle = \int\limits_a^b f(x)g(x)\omega(x)dx,\tag{2.58}\label{eq:2.58} $$ (2.58)

Akkor a $\eqref{eq:2.57}$ egyenletrendszert így alakíthatjuk át:

$$\sum_{k=1}^{n}r_k\left\langle \phi_k(x),\phi_i(x)\right\rangle=\left\langle f(x),\phi_i(x)\right\rangle,\quad i=1,\ldots,n. \tag{2.59}\label{eq:2.59} $$

A Gram-mátrix:

$$\begin{pmatrix} \left\langle \phi_1(x),\phi_1(x)\right\rangle & \cdots & \left\langle \phi_1(x),\phi_n(x)\right\rangle\\ \cdots & \cdots & \cdots \\ \left\langle \phi_n(x),\phi_1(x)\right\rangle & \cdots & \left\langle \phi_n(x),\phi_n(x)\right\rangle \end{pmatrix}\tag{2.60}\label{eq:2.60}$$

alkalmazásával a $\eqref{eq:2.59}$ egyenletrendszert a következő képen írhatjuk le:

$$Gr=p\tag{2.61}\label{eq:2.61}$$

ahol

$$r=(r_1,r_2,\ldots,r_n),\quad p=(p_1,p_2,\ldots,p_n),\quad p_i=\left\langle f(x),\phi_i(x)\right\rangle.$$

Definíció.

A $\{\phi_i(x)\}^n_{i=1}\subset \mathbb{C}[a,b]$ függvény-rendszer ortogonális, ha

$$\left\langle \phi_i(x),\phi_j(x)\right\rangle=0,\quad i,j=1,\ldots, n. \tag{2.62}\label{eq:2.62}$$

A függvény-rendszer ortonormált, ha a $\eqref{eq:2.62}$ feltételek kívül még a

$$\left\langle \phi_i(x),\phi_i(x)\right\rangle=1,\quad i=1,\ldots, n. \tag{2.63}\label{eq:2.63}$$

feltételek is teljesülnek.

Ha a $\{\phi_i(x)\}^n_{i=1}$ ortonormált rendszer, akkor a Gram-mátrix egységmátrix lesz, és egyszerűbb lesz a $q_k$ együtthatók meghatározása:

$$q_k=\left\langle f(x),\phi_k(x)\right\rangle,\quad i=1,\ldots, n. \tag{2.64}\label{eq:2.64}$$

Ezek alapján megkapjuk a legjobb approximációs függvény alakját:

$$\Phi(x)=\sum_{k=1}^{n}\left\langle f(x),\phi_k(x)\right\rangle\phi_k(x),\quad i=1,\ldots, n. \tag{2.65}\label{eq:2.65}$$

A $\eqref{eq:2.62}$ képlet kifejezi a $f(x)$ függvény Fourier-sor első $n$ tagját.

A gyakorlatban több ortonormált függvény-rendszert alkalmaznak.

A legkisebb négyzetek konkrét alkalmazásairól lásd a 9. Fejezetben.

1) Periodikus függvények közelítéséhez alkalmazzák a következő függvény-rendszert:

$$\frac{1}{\sqrt{2\pi}},\, \frac{1}{\sqrt{2\pi}}\cos x,\, \frac{1}{\sqrt{2\pi}}\sin x,\, \frac{1}{\sqrt{2\pi}}\cos 2x,\, \frac{1}{\sqrt{2\pi}}\sin 2x, \ldots\tag{2.66}\label{eq:2.66}$$

$$\omega(x)=1,\quad \mathbb{C}[-\pi,\pi],\,(x\in [-\pi,\pi]). $$

2) Első rendű Csebisev-polinomok $T_n$.

$$\omega(x)=\frac{1}{\sqrt{1-x^2}},\quad \mathbb{C}[-1,1],\,(x\in [-1,1]).$$

Az első rendű Csebisev-polinomot úgy lehet meghatározni, mint a

$$(1 – x^2) y′′(x) – x y′(x) +n y(x) =0 \tag{2.67}\label{eq:2.67}$$

differenciálegyenlet megoldását, ahol $n$ – egész, pozitív.

A Csebisev-polinomok:

$$\frac{1}{\sqrt{2\pi}} T_0,\,\sqrt\frac{2}{\pi}T_n,\, n=1, 2, …\tag{2.68}\label{eq:2.68}$$ ahol

$$T_n(x)=\cos(n\operatorname{arccos}n)\tag{2.69}\label{eq:2.69}$$

vagy másként fogalmazva:

$$T_n(x)=\cos(n\theta),\quad 0\leqslant\theta\pi,\tag{2.70}\label{eq:2.70}$$

és

$$x=\cos \theta .$$

A $T_n(x)$ $n$-ed fokú polinomok, amelyeknek a főegyütthatója mindig $a_n =2^{n–1}$

A definíció alapján kiszámítjuk az első három polinomot:

$$T_0(x) =\cos 0 = 1\tag{2.71}\label{eq:2.71}$$

$$T_1(x)= \cos\theta =x\tag{2.72}\label{eq:2.72}$$

$$T_2(x)= \cos 2\theta = \cos^2\theta - \sin^2\theta = x^2 - (1 - x^2) =2 x^2 -1\tag{2.73}\label{eq:2.73}$$

Csebisev-polinomokat egy rekurzív képletet alapján sokkal kényelmesebb kiszámítani. A definíció szerint

$$T_{n+1}(x)= \cos(nθ +θ) = \cos nθ \cosθ - \sin nθ \sin θ\tag{2.74}\label{eq:2.74}$$

$$T_{n-1}(x)= \cos(nθ -θ) = \cos nθ \cos θ + \sin nθ \sin θ\tag{2.75}\label{eq:2.75}$$

összeadva a (2.74),(2.75) képleteket:

$$T_{n+1}(x)+ T_{n-1}(x)= 2\cos nθ \cosθ =2x T_n(x)\tag{2.76}\label{eq:2.76}$$

a következő rekurzív képletet kapunk:

$$T_{n+1}(x) =2x T_n(x) - T{n-1}(x),\quad n=2, 3, … \tag{2.77}\label{eq:2.77}$$

Ha $n=2$ akkor:

$$T_3(x) =2x T_2(x) - T_1(x)=2x(2x^3 -1) - x =4 x^3 -3\tag{2.78}\label{eq:2.78}$$

Az első rendű Csebisev-polinomok ortonormálisak.

Megmutassuk, hogy az Első rendű Csebisev-polinomok a $[–1, 1]$ intervallumban ortonormálisak. Mivel

$$\int\limits_0^\pi\cos m\theta\cos n\theta d\theta=0,\tag{2.79}\label{eq:2.79}$$

ha $m≠n$,

$$\int\limits_0^\pi\cos m\theta\cos n\theta d\theta=\frac{1}{2}\pi,\tag{2.80}\label{eq:2.80}$$

ha $m=n≠0$,

$$\int\limits_0^\pi\cos m\theta\cos n\theta d\theta=\pi,\tag{2.81}\label{eq:2.81}$$

ha $m=n=0$.

Legyen $x=\cos θ$, akkor

$$\int\limits_{-1}^1(1-x^2)^\frac{1}{2}T_mT_ndx=0,\tag{2.82}\label{eq:2.82}$$ (2.82)

ha $m≠n$,

$$\int\limits_{-1}^1(1-x^2)^\frac{1}{2}T_mT_ndx=\frac{1}{2}\pi,\tag{2.83}\label{eq:2.83}$$

ha $m=n≠0$,

$$\int\limits_{-1}^1(1-x^2)^\frac{1}{2}T_mT_ndx=\pi,\tag{2.84}\label{eq:2.84}$$

ha $m=n=0$.

A (2.82)-(2.84) képletek bizonyítják az Első rendű Csebisev-polinomok ortonolmálisságát.

A $t_n(x)$ polinomokat a Csebisev-polinomok alapján következő képen szerkesztjük.

Legyen

$$t_n(x)=2^{1-n}T_n(x),\quad n =1, 2, \ldots \tag{2.85}\label{eq:2.85}$$

$t_n(x)$ olyan $n$-ed fokú polinomok, amelyeknek a főegyütthatója $a_n=1$ és

$$\max_{x\in[-1,1]}|t_n(x)|=2^{1-n}\tag{2.86}\label{eq:2.86}$$

Tétel.

Az összes $n$-ed fokú és $1$ főegyütthatójú polinomok között a $[-1,1]$ intervallumon vett maximum a $t_n(x)$ polinom esetén minimális.

Az $f(x)$ függvény ortogonális felbontása.

$$f(x)=\sum_{r=0}^n a_rT_r(x),\quad-q\leqslant x\leqslant 1.\tag{2.87}\label{eq:2.87}$$

Akkor

$$a_0=\frac{1}{\pi}\int\limits_{-1}^1(1-x^2)^\frac{1}{2}f(x) dx,\tag{2.88}\label{eq:2.88}$$

$$a_r=\frac{1}{\pi}\int\limits_{-1}^1(1-x^2)^\frac{1}{2}f(x)T_r(x) dx,\tag{2.89}\label{eq:2.89}$$

Ezeket az integrálokat a Csebisev-polinomok tulajdonságai alapján összeg alakba lehet átírni.

Ha

$$x_s=\cos\frac{(2s-1)\pi}{2n}\tag{2.90}\label{eq:2.90}$$

a $T_n(x)$ polinom zérus pontjai, akkor

$$\sum_{s=0}^n T_i(x_s)T_j(x_s)=0, \tag{2.91}\label{eq:2.91}$$

ha $i≠j$.

$$\sum_{s=0}^n T_i(x_s)T_j(x_s)=\frac{n}{2}, \tag{2.92}\label{eq:2.92}$$

ha $i=j≠0$,

$$\sum_{s=0}^n T_i(x_s)T_j(x_s)=n \tag{2.93}\label{eq:2.93}$$

ha $i=j=0$,

$$i<n,\qquad j<n.$$

Innen

$$a_0=\frac{1}{n}\sum_{s=0}^n f(x_s),\tag{2.94}\label{eq:2.94}$$

$$a_0=\frac{2}{n}\sum_{s=0}^n f(x_s)\cos\frac{(2s-1)r\pi}{2n}.\tag{2.95}\label{eq:2.95}$$

2.5. Példa

A következő általános képlet alapján:

$$\sin kx=2\sum_{n=0}^\infty(-1)^n J_{2n+1}(k)T_{2n+1}(x),\tag{2.96}\label{eq:2.96}$$

(ahol a $J_n(x)$ – első rendű Besszel-függvény ($n$ fokú)),

így adhatjuk meg a $\sin x$ függvény közelítését a Csebisev-polinomok által:

$$\sin\left(\frac{\pi x}{2}\right) =1,\!5707963x - 0,\!646336x^3 + 0,\!079688475 x^5 - 0,\!0046722203 x^7 +0,\!000150817 x^9$$

A közelítés hiba-becslése:

$$|R(x)|\leqslant\frac{1}{11!}\left(\frac{\pi x}{2}\right)\leqslant 0,\!0000035988\approx 3,\!6\cdot 10^{-6}.$$

2.6. Példa

$$e^x\approx\sum_{k=0}^7 a_k x^k,\quad-1\leqslant x\leqslant 1,\quad\varepsilon=2\cdot 10^{-7}.$$

$$\begin{equation}\begin{aligned} &a_0 =0,\!9999998 \\ &a_1 =1,\!0000000 \\ &a_2 =0,\!5000063 \\ &a_3 =0,\!1666674 \\ &a_4 =0,\!0416350 \\ &a_5 =0,\!0083298 \\ &a_6 =0,\!0014393 \\ &a_7 =0,\!0002040 \end{aligned}\end{equation}$$ **2.7. Példa** $$\ln(1+x)\approx\sum_{k=0}^7 a_k x^k,\quad 0\leqslant x\leqslant 1,\quad\varepsilon=2,\!2\cdot 10^{-7}.$$ $$\begin{equation}\begin{aligned} &a_1 = \hphantom{-} 0,\!999981028 \\ &a_2 = -0,\!499470150 \\ &a_3 = \hphantom{-} 0,\!338233122 \\ &a_4 = -0,\!225873284 \\ &a_5 = \hphantom{-} 0,\!134639267 \\ &a_6 = -0,\!055119959 \\ &a_7 = \hphantom{-} 0,\!010757369 \end{aligned}\end{equation}$$ A wxMaxima alkalmazása a Csebisev-polinomok előállítására: \\ chebyshev_t(4,x); > $8x^4-8x^2+1$

makelist(printf(true,"T~d(x)=~m~%",n,ratsimp(chebyshev_t(n,x))),n,10)$

T1(x) = $x$
T2(x) = $2x^2-1$
T3(x) = $4x^3-3x$
T4(x) = $8x^4-8x^2+1 $
T5(x) = $16x^5-20x^3+5x $
T6(x) = $32x^6-48x^4+18x^2-1 $
T7(x) = $64x^7-112x^5+56x^3-7x $
T8(x) = $128x^8-256x^6+160x^4-32x^2+1 $
T9(x) = $256x^9-576x^7+432x^5-120x^3+9x $
T10(x) = $512x^{10}-1280x^8+1120x^6-400x^4+50x^2-1 $

wxplot2d([chebyshev_t(2,x),chebyshev_t(3,x),chebyshev_t(5,x)],[x,-1,1],[y,-1,1],
[style,[lines,4]], [legend, "T2(x)", "T3(x)","T5(x)"], [gnuplot_preamble, "set term pngcairo font 'Arial,14';"]);

3) A Legendre-polinomok $P_n(x)$.

Ezeket a polinomokat is gyakran alkalmazzák a függvények közelítésére.

A Legendre-polinomokat úgy határozhatjuk meg, mint a

$$(1 – x^2)y′′(x) – 2xy′(x) + n(n+1)y(x) = 0 \tag{2.97}\label{eq:2.97}$$

differenciálegyenlet megoldását ($n$ – egész, pozitív).

Az $n$-edik Legendre-polinom képlete:

$$ P_n(x)=\frac{1}{2^n n!}\frac{d^n}{dx^n}\left(x^2+1\right)^n=$$

$$=\frac{(2n)!}{2^n n!}\left[x^n-\frac{n(n-1)}{2(2n-1)}x^{n-2}+\frac{n(n-1)(n-2)(n-3)}{2\cdot 4\cdot(2n-1)(2n-3)}x^{n-2}+\ldots\right]\tag{2.98}\label{eq:2.98}$$(2.98)

A $P_n(x)$ polinomok értékei a $0,1,-1$ pontokban:

$$P_n(1) =1,\quad P_n(–1) = (–1)^n,$$ $$P_{2n}(0)=(-1)^n\frac{2n!}{2^{2n}(n!)^2}, P_{2n+1}(0)=0, \tag{2.99}\label{eq:2.99}$$

A Legendre-polinomok konkrét $n$ esetén:

$$\begin{equation}\begin{aligned} &P_0(x) =1 \\ &P_1(x) =x \\ &P_2(x) =\frac{3x^2 - 1}{2} \\ &P_3(x) =\frac{5x^3 - 3x}{2} \\ &P_4(x) =\frac{35x^4 - 30 x^2+3}{8} \\ &P_5(x) =\frac{63x^5 - 70 x^3+15x}{8} \\ &P_6(x) =\frac{321x^6 - 315 x^4+105 x^2-5}{16} \\ \end{aligned}\end{equation}\tag{2.100}\label{eq:2.100}$$ A Legendre-polinomok tulajdonságai. $$P_n(x)=\frac{1}{\pi}\int\limits_0^\pi\left(x\pm\cos t\sqrt {x^2-1}\right)^n dt=\frac{1}{\pi}\tag{2.101}\label{eq:2.101}$$ $$(n+1) P_{n+1}(x) = (2n+1)x P_n(x) – n P_{n-1}(x) \tag{2.102}\label{eq:2.102}$$ (2.102) $$\left(x^2+1\right)\frac{dP_n(x)}{dx}=n[xP_n(x)-P_{n-1}(x)], \tag{2.103}\label{eq:2.103}$$ $$\int\limits_{-1}^1 P_m(x)P_n(x)dx=0\tag{2.104}\label{eq:2.104}$$ ha $m≠n$

$$\int\limits_{-1}^1[P_m(x)]^2 dx=\frac{1}{2m+1}\tag{2.105}\label{eq:2.105}$$

$$F(x, y)=0\tag{2.106}$$

Feltételezzük, hogy az $x$ értéke adott és kell kiszámítani az $y$ értékét. A probléma megoldására a Lagrange-tételt alkalmazzuk, mint a differenciálszámítás első középértéktételét.

Lagrange-tétel.

Ha az $f(x)$ függvény folytonos a véges zárt $[a,b]$ intervallumban és differenciálható a nyitott $(a, b)$-n, akkor létezik olyan belső $c$ pont, hogy

$${\displaystyle f^\prime(c)={\frac {f(b)-f(a)}{b-a}}} \tag{2.107}\label{eq:2.107}$$

A $\eqref{eq:2.107}$ alapján

$$F(x,y)=f(x,y)-{\frac{f(b)-f(a)}{b-a}}(x-a)$$ (2.108)

Feltételezzük, hogy az $F(x, y)$ függvény differenciálható az $y$ változó szerint. Akkor alkalmazva a (2.108) képletet, a következő egyenletet kapunk:

$$F(x, y_0) - F(x, y) = (y_0 -y) F^\prime_y(x, c) \tag{2.109}\label{eq:2.109}$$

A $\eqref{eq:2.109}$-ben $y$ – az ismeretlen, a $y_0$ pedig az $y$ feltételezett értéke.

$$y_0\leqslant c \leqslant y\tag{2.110}\label{eq:2.110}$$

vagy $$y\leqslant c \leqslant y_0\tag{2.111}\label{eq:2.111}$$

Mivel $F(x, z)=0$, akkor

$$F(x, y_0)=(y_0-y) F^\prime y(x, c).\tag{2.112}\label{eq:2.112}$$

Természetesen, a $\eqref{eq:2.112}$ a $c$ értéke ismeretlen. Ezért annak a kezdő értékét csak feltételezhetjük. Legyen az $c≈ y_0$. Akkor kiszámíthatjuk az ismeretlen y közelítő értékét:

$$y= y_0-F(x, y_0)/F^\prime y(x, y_0)\tag{2.113}\label{eq:2.113}$$

De mivel a c értéke nem pontosan volt megadva, ezért a $\eqref{eq:2.113}$ alapján a y értéke is hibát tartalmaz, és ezt az értéket az $y$ csak az első közelítésének tekinthetjük:

$$y_1=y_0-\frac{F(x,y_0)}{F^\prime_y(x,y_0)}.\tag{2.114}\label{eq:2.114}$$

Ha $| y_1 – y_0|<ε$, akkor azt mondatjuk, hogy a $F(x, y)$ függvényt kiértékeltük ε pontossággal. Különben újból végre hajtjuk következő iterációs lépést:

$$y_2=y_1-\frac{F(x,y_1)}{F^\prime_y(x,y_1)}.\tag{2.115}\label{eq:2.115}$$

Hasonlóan folytatva, kapunk egy iterációs folyamatot:

$$\boxed{y_{n+1}=y_n-\frac{F(x,y_n)}{F^\prime_y(x,y_n)}},\tag{2.116}\label{eq:2.116}$$

amelyet addig kell folytatni, amíg nem teljesül a

$$| y_{n+1} - y_n|<ε\tag{2.117}\label{eq:2.117}$$ feltétel.

A (2.116) iterációs folyamat konvergenciájáról.

A (2.116) iterációs eljárás akkor konvergens, ha léteznek olyan deriváltok

$$F^\prime_y(x, y),\quad F^{\prime\prime}_{yy}(x, y),\tag{2.118}\label{eq:2.118}$$

amelyeknek az előjele nem változik.

Konkrét függvények kiértékelése.

2.8. Példa

Vezessük le a $y=\sqrt{x}$ függvény kiértékelésének az iterációs képletét.

$$y^2-x=0$$

$$F^\prime y(x, y)= 2y.$$

Akkor a $\eqref{eq:2.116}$ alapján:

$$y_{n+1}=y_n-\frac{y^2_n-x}{2y_n}=\frac{2y^2_n-y^2_n+x}{2y_n}=\frac{y^2_n+x}{2y_n}$$

a következő iterációs eljárást kapjunk (Heron-képletet):

$$y_{n+1}= \frac{y_n+\displaystyle\frac{x}{y_n} }{2},\quad n=0, 1, \ldots.\tag{2.119}\label{eq:2:119}$$

Ha $y>0$, akkor a $\eqref{eq:2.119}$ iterációs eljárás konvergens, mivel $F^\prime_y(x, y)= 2y>0$, és $F^{\prime\prime}_{yy}(x, y)=2>0$.

2.9. Példa

$$\sqrt{7}=?,\quad\varepsilon=10^{-5}.$$

$$\begin{equation}\begin{aligned} y_0&=2,\\ y_1&=\frac{2+\displaystyle\frac{2}{7}}{2} =2,\!75000, \\ y_2&=\frac{\displaystyle\frac{11}{4}+\displaystyle\frac{28}{11}}{2} =2,\!.64772, \\ y_3&=\frac{233688+\displaystyle\frac{616}{233}}{2} =2,\!.64575, \\ y_4&=\frac{2,\!64575+\displaystyle\frac{7}{2,\!64575}}{2} =2,\!64575. \end{aligned}\end{equation}$$ **2.10. Példa** $$y=\frac{1}{\sqrt{x}}.

Vezessük le a függvény kiértékelésének az iterációs képletét.

$$F(x, y) = y_2 - \frac{1}{x} =0$$

$$F^\prime_y(x, y)= 2y$$

Akkor a $\eqref{eq:2.116}$ alapján

$$y_{n+1}= y_n -\frac{y^2_n-1}{2xy_n} = \frac{xy^2_n+1}{2xy_n}$$

a következő iterációs eljárást kapunk:

$$y_{n+1}= \frac{y_n+\displaystyle\frac{1}{x}y_n}{2},\quad n =0, 1, 2, \ldots.\tag{2.120}\label{eq:2:120}$$

2.11. Példa

$$y=\root{3} \of{x}$$

Vezessük le a függvény kiértékelésének az iterációs képletét.

$$F(x, y) = y^3 – x =0$$

$$F^\prime_y(x, y)= 3y^2$$

Akkor a $\eqref{eq:2.116}$ alapján:

$$y_{n+1}= y_n-\frac{y^3_n-x}{3 y^2} = \frac{2y_n+\displaystyle\frac{x}{y^2}}{3}$$

$$y_{n+1}= \frac{2y_n+\displaystyle\frac{x}{y^2}}{3},\quad n =0, 1, 2, …\tag{2.121}\label{eq:2:121}$$

2.12. Példa

$$y=\sqrt[p]{x}$$

Vezessük le a függvény kiértékelésének az iterációs képletét.

$$x>1,\quad p>0$$

$$F(x, y) = y^p-x =0$$

$$F^\prime_y(x, y) = py^{p-1}$$

Akkor a $\eqref{eq:2.116}$ alapján

$$y_{n+1}= y_n-\frac{y^p_n-x}{p y^{p-1}} = \frac{(p-1) y^p_n +x}{p y^{p-1}_n}$$

a következő iterációs eljárást kapunk:

$$y_{n+1}=\frac{(p-1) y_n +\displaystyle\frac{x}{y^{p-1}_n}}{p},\quad n =0, 1, 2, \ldots.\tag{2.122}\label{eq:2:122}$$

Ha átalakítjuk a $y=\sqrt[p]{x}$ függvényt:

$$F(x, y) =1-\frac{x}{y^p} =0$$

akkor a következő iterációs képletet kapunk:

$$y_{n+1}= y_n\left(\left(1+\displaystyle\frac{1}{p}\right)- \frac{y^p_n}{p}x\right),\quad n =0, 1, 2, …\tag{2.123}\label{eq:2:123}$$

2.13. Példa

Számítsuk ki a $\sqrt[7]{277234}$ értékét $ε=10^{-6}$ pontossággal.

Mivel $p=7$, akkor a $\eqref{eq:2.123}$ alapján:

$$y_{n+1}= y_n\left(\frac{8}{7}-\frac{y^p_n}{7x}\right)$$

Legyen $y_0=6$

$$\begin{equation}\begin{aligned} &y_1= 6\left(\frac{8}{7}-\frac{6^6}{7\cdot 277234}\right)=5,\!99164605 \\[5pt] &y_2=5,\!99169225 \\[5pt] &y_3=5,\!99169225 \\[5pt] &\sqrt[7]{277234}\approx 5,\!99169225 \end{aligned}\end{equation}$$