II. RF KMF DokuWiki

Megfogalmazzuk az interpolációs feladatot.

A

$$x_0< x_1< … < x_n\tag{3.1}\label{eq:3.1}$$

pontokban a $y=f(x)$ függvény értékei adottak:

$$y_k = f_k = f(x_k),\quad k=0, 1, 2, …, n.\tag{3.2}\label{eq:3.2}$$

Általános esetben, nem feltételezzük, hogy a függvény analitikus képlete ismert.

Azt mondjuk, hogy a $P(x)$ interpolációs függvény közelíti az $f(x)$ függvényt, ha

$$P(x_k) = y_k,\quad (k = 0, 1, 2, … , n)\tag{3.3}\label{eq:3.3}$$

$\eqref{eq:3.3}$ – az interpolációs feltételek,

a $\{x_0, x_1, …, x_n \}$ – az interpolációs alappontok (csomópontok).

Természetesen, a $P(x)$ függvénynek olyannak kell lennie, hogy annak az értékeit könnyen lehessen kiszámítani.

Az interpolációs probléma kapcsán a következő kérdéseket kell tisztázni.

1. Hogy kell kiválasztani az $x_0, x_1, …, x_n$ alappontokat. Sok gyakorlati feladat esetén az alappontok már adottak, és nincs szükség ezzel a kérdéssel foglalkozni.
2. Milyen függvény-osztályból választjuk ki a $P(x)$ függvényeket.
3. Milyen lesz a $|f(x)-P(x)|$ maximális értéke, a módszer-hiba.

Ha a $P(x)$ függvényt a $(x_0, x_n)$ intervallumon kívül keressük, akkor ezt a feladatot extrapolációnak nevezzük.

A $P(x)$ interpolációs függvény alakját a

$$ P(x)=a_0\varphi_0(x)+a_1\varphi_1(x)+\ldots+ a_n\varphi_n(x)=\sum_{k=1}^n a_k\varphi_k(x) \tag{3.4}\label{eq:3.4}$$

formában keressük, ahol a

$$\{φ_0(x), φ_1(x), …, φ_n(x)\}$$ – bázisfüggvény-rendszer.

A $φ_k(x)$ ismert függvények, az $a_0, a_1, … , a_n$ együtthatók ismeretlenek, és a $\eqref{eq:3.3}$ interpolációs feltételekből lehet azokat meghatározni: $$\begin{equation}\begin{aligned} &a_0φ_0(x_0) + a_1φ_1(x_0) + a_nφ_n(x_0) = f(x_0),\\ &a_0φ_0(x_1) + a_1φ_1(x_1) + a_nφ_n(x_1) = f(x_1),\\ &.......................................\\ &a_0φ_0(x_n) + a_1φ_1(x_n) + a_nφ_n(x_n) = f(x_n).\\ \end{aligned}\end{equation}\tag{3.5}\label{eq:3.5}$$ Ha ennek az egyenletrendszernek a determinánsa $≠0$, akkor az egyenletrendszernek pontosan egy megoldása van, amelyet például, így lehet meghatározni

$$a_i = \frac{Δ_i}{Δ},\quad i = 0, 1, … , n \tag{3.6}\label{eq:3.6}$$ ahol

$$\Delta=\begin{vmatrix} \varphi_0(x_0) & \varphi_1(x_0) & \cdots & \varphi_n(x_0)\\ \varphi_0(x_1) & \varphi_1(x_1) & \cdots & \varphi_n(x_1)\\ \cdots & \cdots & \cdots & \cdots \\ \varphi_0(x_n) & \varphi_1(x_n) & \cdots & \varphi_n(x_n) \end{vmatrix}\neq 0 \tag{3.7}\label{eq:3.7}$$

$$\Delta_i=\begin{vmatrix} \varphi_0(x_0) & f(x_0) & \cdots & \varphi_n(x_0)\\ \varphi_0(x_1) & f(x_1) & \cdots & \varphi_n(x_1)\\ \cdots & \cdots & \cdots & \cdots \\ \varphi_0(x_n) & f(x_n) & \cdots & \varphi_n(x_n) \end{vmatrix}.\tag{3.8}\label{eq:3.8}$$

Akkor

$$P(x) = \frac{φ_0(x) Δ_0 + φ_1(x) Δ_1 + … + φ_n(x) Δ_n}{Δ}\tag{3.9}\label{eq:3.9}$$ és az együtthatókat így lehet kifejezni:

$$a_i=\frac{\displaystyle\sum_{j=0}^n f(x_j)\Delta_{ij} }{\Delta},\quad i=0,1,\ldots,n,\tag{3.10}\label{eq:3.10}$$

ahol a $Δ_{ij}$ – a mátrix algebrai komplementerei.

A $\{φ_0(x), φ_1(x), …, φ_n(x)\}$ bázisfüggvényeket többféle képen lehet kiválasztani. Fontos, hogy a kiválasztott függvény-rendszer lineárisan független legyen. Leggyakrabban a következő bázisfüggvényeket szoktak alkalmazni:

$$\{1, x, x_2, …, x_n, …\}$$

$$\{1, \sin x, \cos x, \sin x^2, \cos x^2, …\}$$

$$\{1,e^x, e^{2x}, …\}$$

A Lagrange-féle interpolációs polinom a

$$\{1, x, x_2, …, x_n, …\}\tag{3.11}\label{eq:3.11}$$

bázisfüggvények alapján vannak szerkesztve. A (3.11) függvény-rendszer lineárisan független, mivel $$c_0 + c_1x+ c_2x^2 + … +c_nx^n =0,\quad x\in[x_0,x_n]\tag{3.12}\label{eq:3.12}$$

csak akkor, ha az összes

$$c_i=0, i= 0, 1, … , n.$$

A (3.11) függvény-rendszer alapján szerkesztet (3.7) determináns:

$$\Delta=\begin{vmatrix} 1 & x_0 & \cdots & x^n_0\\ 1 & x_1 & \cdots & x^n_1\\ \cdots & \cdots & \cdots & \cdots \\ 1 & x_n & \cdots & x^n_n \end{vmatrix}=\prod_{i>j}(x_i-x_j)\neq 0 \tag{3.13}\label{eq:3.13}$$

az ismert Wandermonde-determináns.

A Lagrange-féle interpolációs polinomot a következő alakban keressük:

$$L^{(n)}(x) = L_0(x)y_0 + L_1(x)y_1 + L_2(x)y_2 + … L_n(x)y_n\tag{3.14}\label{eq:3.14}$$

ahol $L_k(x)$ a Lagrange-féle együtthatók.

Az interpolációs feltételek alapján:

$$L_0(x_k)y_0 + L_1(x_k)y_1 + L_2(x_k)y_2 + …+L_n(x_k)y_n=y_k, \quad k = 0, 1, … , n\tag{3.15}\label{eq:3.15}$$

vagy

$$\begin{equation}\begin{aligned} &L_0(x_0)y_0 + L_1(x_0)y_1 + L_2(x_0)y_2 + … + L_n(x_0)y_n= y_0 \\ &L_0(x_1)y_0 + L_1(x_1)y_1 + L_2(x_1)y_2 + … + L_n(x_1)y_n= y_1 \\ &...................................................\\ &L_0(x_n)y_0 + L_1(x_n)y_1 + L_2(x_n)y_2 + … + L_n(x_n)y_n=y_n \end{aligned}\end{equation}\tag{3.16}\label{eq:3.16}$$ Megköveteljük, hogy a $L_i(x_k)$ együtthatók az alappontokban a következő értékeket vegyenek fel:

$$L_i(x_k) =0,\,\text{ ha } k ≠i\tag{3.17}\label{eq:3.17}$$

$$L_i(x_k) =0,\,\text{ ha } k=i\tag{3.18}\label{eq:3.18}$$

$$i, k = 0, 1, …, n$$

Mivel a (3.17) alapján a $x_k$, (ha $k ≠i$) – a $L_i(x)$ gyökei, akkor:

$$L_i(x) = C(x-x_0)(x-x_1)\cdot\ldots\cdot(x-x_{i-1})(x-x_{i+1})\cdot\ldots\cdot(x-x_n) \tag{3.19}\label{eq:3.19}$$

A C konstans értékét megállapíthatjuk a (3.18) feltételekből:

$$L_i(x_i)=C(x_i-x_0)(x_i-x_1)\cdot\ldots\cdot(x_i-x_{i-1})(x_i-x_{i+1})\cdot\ldots\cdot(x_i-x_n)=1 \tag{3.20}\label{eq:3.20}$$

$$C=\frac{1}{[(x_i-x_0)(x_i-x_1)·…·(x_i-x_{i-1})(x_i-x_{i+1})·…·(x_i-x_n)]} \tag{3.21}\label{eq:3.21}$$

Ez alapján a Lagrange-féle együtthatók:

$$L_i^{(n)}=\displaystyle\frac{(x-x_0)(x-x_1)\cdot\ldots\cdot(x-x_{i-1})(x-x_{i+1})\cdot\ldots\cdot(x-x_n)} {(x_i-x_0)(x_i-x_1)·…·(x_i-x_{i-1})(x_i-x_{i+1})·…·(x_i-x_n)} \tag{3.22}\label{eq:3.22}$$

Tehát, megkaptuk a Lagrange-féle interpolációs polinom képletét:

$$L^{(n)}=\sum_{i=0}^n\displaystyle\frac{(x-x_0)(x-x_1)\cdot\ldots\cdot(x-x_{i-1})(x-x_{i+1})\cdot\ldots\cdot(x-x_n)} {(x_i-x_0)(x_i-x_1)·…·(x_i-x_{i-1})(x_i-x_{i+1})·…·(x_i-x_n)}\cdot y_i\tag{3.23}\label{eq:3.23}$$

Ezt a képletet úgy átalakíthatjuk, hogy könnyen lehessen kiértékelni az interpolációs polinomot.

Az alappontokból a következő táblázatot készítünk: $$\begin{matrix} x-x_0 & x_0-x_1 & x_0-x_2 & … & x_0-x_n \\ x_1-x_0 & x-x_1 & x_1 - x_2 & … & x_1-x_n \\ x_2-x_0 & x_2-x_1 & x - x_2 & … & x_2-x_n \\ … & … & … & … & … \\ x_n-x_0 & x_n-x_1 & x_n-x_2 & … & x-x_n \end{matrix}\tag{3.24}\label{eq:3.24}$$

A Lagrange-féle együtthatókat a

$$L_i(x) = \frac{ω_n(x)}{D_i},\quad i = 0, 1, …, n \tag{3.25}\label{eq:3.25}$$

képletek alapján lehet kiszámítani, ahol

$$ω_n(x)= (x- x_0) (x- x_1)\cdot\ldots\cdot(x-x_n) \tag{3.26}\label{eq:3.26}$$

a $D_i$ pedig a (3.24) táblázat i-ik sorának elemeinek szorzata.

A Lagrange-féle együtthatókat egy másik képlet alapján is kiszámíthatjuk. A (3.27) deriválása

$$ω′_n(x)= (x-x_1)(x-x_2)\cdot\ldots\cdot(x-x_n)+(x-x_0)(x-x_2)\cdot\ldots\cdot(x-x_n)+\ldots (x-x_0)(x-x_1)\cdot\ldots\cdot(x-x_{n-1}) \tag{3.27}\label{eq:3.27}$$ és

$$ω′_n(x)= (x_i- x_0) (x_i- x_1)·…\cdot (x_i- x_{i-1}) (x_i- x_{i+1})… (x_i- x_n) \tag{3.28}\label{eq:3.28}$$

alapján a következő képletet kapunk.

$$L(x)=\sum_{i=0}^n\frac{\omega_n(x)}{(x-x_i)\cdot\omega^\prime_n(x_i)}\cdot y_i \tag{3.29}\label{eq:3.29}$$

A Lagrange-féle interpolációs polinom hiba-becslése:

$$f(x)-L(x)=\frac{f^{(n+1)}(x_i)}{(n+1)!}\omega_n(x) \tag{3.30}\label{eq:3.30}$$

$$R_n(x)=|f(x)-L(x)|\leqslant\frac{M_{n+1}}{(n+1)!}|\omega_n(x)| \tag{3.31}\label{eq:3.31}$$

ahol

$$M_{n+1}=\max_{x\in[a,b]}\left|f^{(n+1)}(x)\right| \tag{3.32}\label{eq:3.32}$$ (3.32)

3.1. Példa

A $100$, $101$, $102$, $103$ pontokban kiszámítottuk a $ln x$ függvény értékeit. Okkor milyen pontossággal lehet kiszámítani a Lagrange-féle interpolációs polinom segítségével a $ln 100,\!5$ értékét?

$$n=3,\quad a =100,\quad b =103$$

$$f(x) =\ln x \quad f′(x)=\frac{1}{x} \quad f′′ (x)= -\frac{1}{x^2} \quad f′′′ (x)=\frac{2}{x^3}$$

$$f^{(4)}(x)= -\frac{6}{x^4} \quad M_4=\frac{6}{100^4}$$

$$|\ln 100,\!5 - L(100,\!5)| \leqslant \frac{6}{4!·100^4} ·0,\!5·0,\!5·1,\!5·2,\!5 =2,\!344·10^{-9}.$$

Javasoljuk megoldani a 10. Fejezetben található feladatokat.

Példa.

Írjunk wxMaxima eljárást a Lagrange-féle interpolációs polinom meghatározására (a Maxima interpol csomagja tartalmazza a lagrange(x) parancsot a polinomiális interpoláció alkalmazására).

(%i1) lagrange_polinom(ptxy):=block(
  n:length(ptxy),
  s:0, 
  for i:1 thru n do (block(
    p:ptxy[i][2],
    for j:1 thru n do(
      if(i#j) then
        p:p*(x-ptxy[j][1])/(ptxy[i][1]-ptxy[j][1])
        ),s:s+p
  )),
  return (s)
)$

(%i2)	pontok:[[0,0],[1,1],[2,4]];
(%o2)	[[0,0],[1,1],[2,4]]

(%i3)	lagrange_polinom(pontok);
(%o4)	2*(x-1)*x-(x-2)*x

(%i4)	%,expand;
(%o4)	x^2 

Feltételezzük, hogy

$$x_{k+1} - x_k = h,\quad k =0, 1, …, n -1 \tag{3.33}\label{eq:3.33}$$

Ha bevezetünk új változót:

$$t=\frac{x - x_0}{h}\tag{3.34}\label{eq:3.34}$$ akkor

$$x - x_0 = th\tag{3.35}\label{eq:3.35}$$ és

$$x - x_1= x - x_0 - (x_1 - x_0)= th - h = h(t -1) \tag{3.36}\label{eq:3.36}$$

$$x - x_k= x - x_0 - (x_k - x_0)= th -kh = h(t - k) \tag{3.37}\label{eq:3.37}$$

Mivel

$$x_{k+j} - x_k = h_j\tag{3.38}\label{eq:3.38}$$

akkor

$$\begin{equation}\begin{aligned} L_i(x)&=\frac{th(th-h)\ldots\left((th-(i-1)h)\right)\left((th-(i+1)h)\right)\ldots(th-nh)}{ih\cdot(i-1)h\cdot\ldots\cdot h(-h)(-2h)\ldots(-(n-i)h)}=\\ &=\frac{t(t-1)\ldots()}{t-i}\cdot\frac{(-1)^{n-i}}{i!\cdot(n-i)!}=(-1)^{n-i}C_n^i\frac{1}{t-i}, \end{aligned}\end{equation}\tag{3.39}\label{eq:3.39}$$ ahol a $C_n^i={i\choose n}$.

Tehát, a Lagrange-féle interpolációs polinom, ekvidisztáns alappontok esetén:

$$L(x)=L(x_0+th)=\sum_{i=0}^nL_i(t)y_i,\tag{3.40}\label{eq:3.40}$$

ahol a Lagrange-féle együtthatók:

$$\boxed{L_i(t)=(-1)^{n-i}C_n^i\frac{1}{t-i}\cdot\frac{t(t-1) \ldots(t-n)}{n!} }\tag{3.41}\label{eq:3.41}$$

nem függnek a $f(x)$ és a $h$ értékeitől.

3.2. Példa

$$\begin{array}{ccc} n=3 & & & & \\ x_i & 0 & 0,\!1 & 0,\!3 & 0,\!5 \\ y_i & -0,5 & 0 & 0,\!2 & 1 \end{array}$$

$$L_0(x)=\frac{}{(-0,\!1)(-0,\!3)(-0,\!5)}=\frac{}{0,\!015}$$

$$L_2(x)=\frac{}{(-0,\!1)(-0,\!3)(-0,\!5)}=\frac{}{0,\!012}$$

$$L_3(x)=\frac{}{(-0,\!1)(-0,\!3)(-0,\!5)}=\frac{}{0,\!04}$$

$$L^{(3)}(x) = L_0(x)y_0 + L_2(x)y_2 + L_3(x)y_3 = \frac{125}{3}·x^3 + 30·x^2+\frac{73}{12}·x - 0,\!5.$$

Ha a $y_0, y_1, …, y_n$ függvény értékei adva vannak, akkor azok alapján $n$ elsőrendű differenciát szerkeszthetünk:

$$Δy_i = y_{i+1} - y_i,\quad i =0, 1, …, n-1 \tag{3.42}\label{eq:3.42}$$

A differenciákat másképp is jelölhetjük:

$$Δy_i = \frac{f^1_{i+1} }{2}\tag{3.43}\label{eq:3.43}$$

Az elsőrendű differenciából $n-1$ másodrendű differenciát lehet létrehozni:

$$Δ^2y_i=Δy_{i+1} - Δy_i\tag{3.44}\label{eq:3.44}$$

vagy a másik jelölésben:

$$f^2_{i+1/2} = f^1_{i+1/2} - f^1_{i-1/2} \tag{3.45}\label{eq:3.45}$$

Így folytatva, szerkeszthetünk $k$-rendű differenciákat:

$$Δ^ky_i= Δ^{k-1}y_{i+1} - Δ^{k-1}y_i \tag{3.46}\label{eq:3.46}$$

3.3. Példa

$$f(x) = x^3$$

Differenciák: $$\begin{array}{ccccc} x & f(x) & f^1 & f^2 & f^3 \\ 0 & 0 & & & \\ & & 1 & & \\ 1 & 1 & & 6 & \\ & & 7 & & 6 \\ 2 & 8 & & 12 & \\ & & 19 & & 6 \\ 3 & 27 & & 18 & \\ & & 37 & & 6 \\ 4 & 64 & & 24 & \\ & & 61 & & \\ 5 & 125 & & & \end{array}$$

Adva vannak a $\{ x_0, x_1, …, x_n\}$ – az interpolációs alappontok, és ezekben a pontokban a függvény értékei:

$$\{ f(x_0), f(x_1), …, f(x_n) \}$$

Akkor szerkeszthetünk $n$ elsőrendű osztott differenciát:

$$\begin{equation}\begin{aligned} f(x_0, x_1) &= \frac{f(x_1) - f(x_0)}{x_1 -x_0},\\ f(x_1, x_2) &= \frac{f(x_2) - f(x_1)}{x_2 -x_1},\\ \cdots & \cdots\cdots\cdots\cdots \\ f(x_{n-1}, x_n) &= \frac{f(x_n) - f(x_{n-1})}{x_n -x_{n-1}}. \end{aligned}\end{equation}\tag{3.47}\label{eq:3.47}$$ Az elsőrendű osztott differenciák alapján $n-1$ másodrendű osztott differenciát lehet létrehozni: $$\begin{equation}\begin{aligned} f(x_0, x_1, x_2) &= \frac{f(x_1, x_2) - f(x_0, x_1)}{x_2 -x_0}\\ f(x_1, x_2, x_3) &= \frac{f(x_2, x_3) - f(x_1, x_2)}{x_3 -x_1}\\ \cdots & \cdots\cdots\cdots\cdots\cdots \\ f(x_{n-2}, x_{n-1}, x_n) &= \frac{f(x_{n-1},x_n)-f(x_{n-2}, x_{n-1})}{x_n -x_{n-2}} \end{aligned}\end{equation}\tag{3.48}\label{eq:3.48}$$ A $k$-rendű osztott differenciákat így kapjuk:

$$f(x_i, x_{i+1},…, x_{i+k}) = \frac{f(x_{i+1}, x_{i+2},…, x_{i+k}) - f(x_i, x_{i+1},…, x_{i+k-1})}{x_{i+k} -x_i}\tag{3.49}\label{eq:3.49}$$

Az osztott differenciákat egy másik jelölése:

$$[x_i, x_{i+1},…, x_{i+k}]\tag{3.50}\label{eq:3.50}$$

3.4. Példa

$$f(x) = x^3$$

Osztott differenciák:

$$\begin{array}{ccccc} x & f(x) & [x_i, x_{i+1}] & [x_i, x_{i+1},x_{i+2}] & [x_i, x_{i+1}, x_{i+2}, x_{i+3}] \\ 0 & 0 & & & \\ & & 4 & & \\ 2 & 8 & & 5 & \\ & & 19 & & 1 \\ 3 & 27 & & 10 & \\ & & 49 & & 1 \\ 5 & 125 & & 14 & \\ & & 91 & & 1 \\ 6 & 216 & & 12 & \\ & & 43 & & \\ 1 & 1 & & & \end{array}$$

A következő tétel tartalmazza az osztott differenciák fontos tulajdonságát.

Tétel

$$f(x_i, x_{i+1},…, x_{i+k}) = \frac{f(x_i)}{(x_i - x_{i+1}) (x_i - x_{i+2})… (x_i - x_{i+k})} + $$

$$+\frac{f(x_{i+1})}{(x_{i+1} - x_i) (x_{i+1} - x_{i+2})… (x_i -x_{i+k}) } + … +$$

$$+\frac{f(x_{i+k})}{(x_{i+k} - x_i) (x_{i+k} - x_{i+1})… (x_{i+k} - x_{i+k-1}) }\tag{3.51}\label{eq:3.51}$$

Ha az interpolációs alappontok ekvidisztánsak, akkor a differenciák és az osztott differenciák között a következő kapcsolat létezik:

$$f(x_i, x_{i+1}) =\frac{f_{i+1} - f_i}{x_{i+2} - x_i} = \frac{Δy_i}{h} = \frac{f^1_{i+\frac{1}{2}}}{h}$$

$$f(x_i, x_{i+1}, x_{i+2}) =\frac{f(x_{i+1}, x_{i+2}) - f_i(x_i, x_{i+1})}{x_{i+2} - x_i} = \frac{Δy_i}{h} = \frac{f^1_{i+\frac{1}{2}}}{h}$$

$$f(x_i, x_{i+1}, x_{i+2}) =\frac{f(x_{i+1}, x_{i+2}) - f_i(x_i, x_{i+1})}{x_{i+2} - x_i} = \frac{Δ^2y_i}{2h^2} = \frac{f^2_{i+1}}{2h^2}.$$

Teljes matematikai indukció alkalmazásával a következő általános képletet lehet bebizonyítani:

$$ \boxed{f(x_i, x_{i+1},\ldots,x_{i+k}) = \frac{Δ^ky_i}{k!h^k} = \frac{f^k_{i+\frac{k}{2}}}{k!h^k} } \tag{3.52}\label{eq:3.52}$$

A Newton-féle interpolációs polinomot a következő alakban keressük:

$$N_n(x)=b_0+b_1(x-x_0)+b_2(x-x_0)(x-x_1)+\ldots+b_b(x-x_0)(x-x_1)\ldots(x-x_{n-1})\tag{3.53}\label{eq:3.53}$$

Az interpolációs feltételek alapján a kővetkező lineáris egyenletrendszert kapunk

$$\begin{equation}\begin{array}{lr} b_0 &=y_1\\ b_0+b_1(x_1-x_0) &=y_2\\ b_0+b_1(x_2-x_0)+b_2(x_2-x_0)(x_2-x_1) &=y_3\\ \cdots\cdots & \\ b_0+b_1(x_2-x_0)+b_2(x_2-x_0)(x_2-x_1)+\ldots + b_n(x_n-x_0)(x_n-x_1)\ldots(x_n-x_{n-1}) &=y_n \end{array}\end{equation}\tag{3.54}\label{eq:3.54}$$ A (3.54) egyenletrendszer determinánsa: $$\begin{equation}\Delta=\begin{vmatrix} 1 & 0 & 0 & \cdots & 0 \\ 1 & x_1-x_0 & 0 & \cdots & 0 \\ 1 & x_2-x_0 & (x_2-x_0)(x_2-x_1) & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & x_n-x_0 & (x_n-x_0)(x_n-x_1) &\cdots & \displaystyle\prod_{k=0}^n(x_n-x_k)\\ \end{vmatrix}\neq 0\end{equation}\tag{3.55}\label{eq:3.55}$$ MATH (3.55) Ez az egyenletrendszer könnyen megoldható, mivel a mátrixa háromszögű. A Lagrange-féle interpolációs polinomok alkalmazásával létrehozzuk a Newton-féle interpolációs polinomot: $$L^{(n)}(x)=L^{(0)}(x)+[L^{(1)}(x)-L^{(0)}(x)] +[L^{(2)}(x)-L^{(1)}(x)]+\ldots+[L^{(n)}(x)-L^{(n-1)}(x)] \tag{3.56}\label{eq:3.56}$$ MATH (3.56) ahol $L^{(k)}(x)-L^{(k-1)}(x)$ a $k$-fokú Lagrange-féle interpolációs polinom:

$$L^{(k)}(x)-L^{(k-1)}(x)=A(x-x_0)\ldots(x-x_{k-1}) \tag{3.57_1}\label{eq:3.57_1}$$ MATH (3.57)

ha $x=x_{k}$, akkor

$$f(x_k)-L^{(k-1)}(x)=f(x_k)-\sum_{j=0}^{k-1} f(x_j) \frac{(x_k-x_0)\cdot\ldots\cdot(x_k-x_{j-1})(x_k-x_{j+1}) \cdot\ldots\cdot(x_k-x_{k-1})} {(x_j-x_0)\cdot\ldots\cdot(x_j-x_{j-1})(x_j-x_{j+1})\cdot\ldots\cdot(x_j-x_{k-1})}=A(x_k-x_0)\ldots(x_k-x_{k-1}) \tag{3.57}\label{eq:3.57}$$ MATH (3.57)

és az $A$ értéke:

$$\begin{matrix} A=\displaystyle\frac{f(x_k)}{(x_k-x_0)\ldots(x_k-x_{k-1})}+\frac{\displaystyle\sum_{j=0}^{k-1} f(x_j) \frac{(x_k-x_0)\ldots(x_k-x_{j-1})(x_k-x_{j+1})\ldots\cdot(x_k-x_{k-1})} {(x_j-x_0)\ldots(x_j-x_{j-1})(x_j-x_{j+1})\ldots(x_j-x_{k-1})} }{(x_k-x_0)\ldots(x_k-x_{k-1})}=\\ =\displaystyle\sum_{j=0}^{k}\frac{f(x_j)}{(x_j-x_0)\ldots(x_j-x_{j-1})(x_j-x_{j+1})\ldots(x_j-x_{k-1})} \end{matrix}\tag{3.58}\label{eq:3.58}$$ MATH (3.58)

Akkor az osztott differenciák tulajdonsága alapján:

$$A=f(x_0, x_1, … , x_n)\tag{3.59}\label{eq:3.59}$$ (3.59)

és a Newton-féle interpolációs polinom képletét így lehet meghatározni:

MATH

$$\begin{equation}\begin{aligned} N^{(x)}(x)&=f(x_0)+(x-x_0)f(x_0,x_1)+(x-x_0)(x-x_1)f(x_0,x_1,x_2)+ \\ &\ldots+(x-x_0)(x-x_1)\ldots(x-x_{n-1})f(x_0,x_1,\ldots,x_n) \end{aligned}\end{equation} \tag{3.60}\label{eq:3.60}$$ MATH(3.60) $$N^{(x)}(x)=f(x_0)+\sum_{j=1}^{n}\left[\prod_{k=0}^{j-1}(x-x_k)\right]f(x_0,x_1,\ldots,x_j) \tag{3.61}\label{eq:3.61}$$ MATH (3.61) A //Newton-féle interpolációs polinom hiba-becslése// megegyezik a Lagrange-féle interpolációs polinom hiba-becsléssel. A hiba-becslést egy másik alakban az osztott differenciák tulajdonsága alapján lehet megadni. A osztott differenciák tulajdonsága alapján: MATH $$\begin{equation}\begin{array}{c} f(x,x_0,x_1,\ldots,x_n)=\displaystyle\frac{f(x)}{(x-x_0)(x-x_1)\ldots(x-x_n)}+\displaystyle\frac{f(x_0)}{(x_0-x)(x_0-x_1)\ldots(x_0-x_n)}+\\+\ldots+\displaystyle\frac{f(x_n)}{(x_n-x_0)(x_n-x_1)\ldots(x_n-x_{n-1})} \end{array}\end{equation}\tag{3.62}\label{eq:3.62}$$ MATH (3.62) ahonnan MATH $$\begin{equation}\begin{array}{c} f(x)=f(x_0)\displaystyle\frac{(x-x_1)(x-x_2)\ldots(x-x_n)}{(x_0-x_1)(x_0-x_2)\ldots(x_0-x_n)}+ f(x_1)\displaystyle\frac{(x-x_0)(x-x_2)\ldots(x-x_n)}{(x_1-x_0)(x_1-x_2)\ldots(x_1-x_n)}+\ldots \\ +f(x_n)\displaystyle\frac{(x-x_1)(x-x_2)\ldots(x-x_{n-1})}{(x_n-x_0)(x_n-x_1)\ldots(x_n-x_{n-1})}+(x-x_0)(x-x_1)\ldots(x-x_n)f(x,x_0,x_1,\ldots,x_n) \end{array}\end{equation} \tag{3.63}\label{eq:3.63}$$ MATH (3.63) $$f(x)=L_n(x)+(x-x_0)(x-x_1)\ldots(x-x_n)f(x,x_0,x_1,\ldots,x_n)\tag{3.64}\label{eq:3.64}$$ MATH (3.64) $$R_n(x)=f(x)-L_n(x)+(x-x_0)(x-x_1)\ldots(x-x_n)f(x,x_0,x_1,\ldots,x_n)\tag{3.65}\label{eq:3.65}$$ MATH (3.65) mivel $$f(x,x_0,x_1,\ldots,x_n)=\frac{f^{(n+1)}(\xi)}{(n+1)!}\tag{3.66}\label{eq:3.66}$$ MATH (3.66) és $$\omega(x)=(x-x_0)(x-x_1)\ldots(x-x_n)\tag{3.67}\label{eq:3.67}$$ MATH (3.67) $$M_{n+1}=\max_{x\in[a,b]}\left|f^{(n+1)}(x)\right|\tag{3.68}\label{eq:3.68}$$ MATH (3.68) $$f(x)-L_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}\omega_n(x)\tag{3.69}\label{eq:3.69}$$ MATH (3.69) akkor a //Newton-féle interpolációs polinom hiba-becslése//: $$\begin{equation}\boxed{R_n(x)=\left|f(x)-L_n(x)\right|\leqslant \frac{M_{n+1}}{(n+1)!}|\omega_n(x)|}\end{equation}\tag{3.70}\label{eq:3.70}$$ MATH (3.70) **3.5. Példa** $$X=(0, 2, 3, 5);\quad Y=(1, 3, 2, 5);$$ $$f(x_{i},x_{i+1})=\left(1, 0,\!1, \frac{3}{2}\right)$$ MATH $$f(x_{i},x_{i+1},x_{i+2})=\left(-\frac{2}{3}, \frac{5}{6}\right)$$ MATH $$f(x_{i},x_{i+1},x_{i+2},x_{i+3})=\frac{3}{10}$$ $$L_3(x)=1+x+\left(-\frac{2}{3}\right)(x-2)x+\frac{3}{10}x(x-2)(x-3)$$ ==== 3.7. Első Newton-féle interpolációs polinom. Ekvidisztáns alappontok esete ==== A (3.60) és (3.52) képletek alapján a kővetkező képletet kapunk: $$N_n(x)=f_0+\frac{x-x_0}{h}f^1_{\frac{1}{2}}+\frac{(x-x_0)(x-x_1)}{2!\cdot h^2}f^2_1+\frac{(x-x_0)(x-x_1)(x-x_2)}{3!\cdot h^3}f^3_{\frac{3}{2}}+\ldots+\frac{(x-x_0)\ldots(x-x_{n-1})}{n!\cdot h^n}f^n_{\frac{n}{2}} \tag{3.71}\label{eq:3.71}$$ MATH (3.71) vagy a differenciák másik jelölését alkalmazva: $$N_n(x)=f_0+\frac{x-x_0}{h}\Delta y_0+\frac{(x-x_0)(x-x_1)}{2!\cdot h^2}\Delta^2y_0+\ldots+\frac{(x-x_0)\ldots(x-x_{n-1})}{n!\cdot h^n}\Delta^ny_0\tag{3.72}\label{eq:3.72}$$ MATH (3.72) Ha bevezetünk új $t$ változót, akkor a képletet kényelmesebb formába hozhatjuk:

$$t=\frac{x-x_0}{h},\tag{3.73}\label{eq:3.73}$$ (3.73)

akkor

$$x=x_0+t\cdot h,$$

és

MATH $$x-x_0=t\cdot h,\quad x-x_1=(t-1)h,\quad\ldots\quad x-x_n=(t-n)h \tag{3.74}\label{eq:3.74}$$ MATH (3.74)

Ha ez alapján átalakítjuk a (3.71) és (3.72) képleteket, akkor a következő képleteket kapunk:

Az első Newton-féle interpolációs képlete az ekvidisztáns alappontok esetén:

$$N^{(n)}_1(x)=f_0+tf^1_{\frac{1}{2}}+\frac{t(t-1)}{2!}f^2_1+\frac{t(t-1)(t-2)}{3!}f^3_{\frac{3}{2}}+\ldots+\frac{t(t-1)\ldots(t-(n-1))}{n!}f^n_{\frac{n}{2}} \tag{3.75}\label{eq:3.75}$$ MATH (3.75)

vagy a másik jelölés alkalmazásával: $$N^{(n)}_1(x)=y_0+t\Delta y_0+\frac{t(t-1)}{2!}\Delta^2y_0+\frac{t(t-1)(t-2)}{3!}\Delta^3y_0+\ldots+\frac{t(t-1)\ldots(t-(n-1))}{n!}\Delta^ny_0 \tag{3.76}\label{eq:3.76}$$ MATH (3.76)

Ha $n=1$, akkor lineáris interpolációs képletet kapunk:

$$y(x)=y_0+t\Delta y_0\tag{3.77}\label{eq:3.77}$$

MATH (3.77)

A kvadratikus (négyzetes) interpolációs képlete ($n=2$):

$$y(x)=y_0+t\Delta y_0+\frac{t(t-1)}{2!}\Delta^2y_0 \tag{3.78}\label{eq:3.78}$$ MATH (3.78)

A hiba-becslés (maradék-tag) két alakja:

$$R_n(x)=h^{n+1}t(t-1)\ldots(t-n)\frac{f^{(n+1)}(\xi)}{(n+1)!} \tag{3.79}\label{eq:3.79}$$ MATH (3.79)

és $$R_n(x)\approx t(t-1)\ldots(t-n)\frac{\Delta^{n+1}y_0}{(n+1)!} \tag{3.80}\label{eq:3.80}$$ MATH (3.80)

3.6. Példa

A $y=\lg x$ függvény táblázat formában van megadva. Számítsuk ki a $\lg 1001$ értékét.

$$\begin{matrix} x & y & \Delta y & \Delta^2y & \Delta^3y \\ 1000 & 3,\!0000000 & 0,\!0043214 & -0,\!0000426 & 0,\!0000008 \\ 1010 & 3,\!0043214 & 0,\!0042788 & -0,\!0000418 & 0,\!0000009 \\ 1020 & 3,\!0086002 & 0,\!0042370 & -0,\!0000407 & 0,\!0000008 \\ 1030 & 3,\!0128372 & 0,\!0041961 & -0,\!0000401 & \\ 1040 & 3,\!0170333 & 0,\!0041560 & & \\ 1050 & 3,\!0211893 & & & \\ \end{matrix} $$

$$y(x)=y_0+t\Delta y_0+\frac{t(t-1)}{2!}\Delta^2y_0+\frac{t(t-1)(t-2)}{3!}\Delta^3y_0 $$

ha $x=1001$, akkor

$$t=\frac{1001-1000}{10}=0,\!1.$$

$$\lg 1001=3,\!00000000+0,\!1\cdot 0,\!0043214+\frac{0,\!1\cdot 0,\!9}{2}0,0000425+\frac{0,\!1\cdot 0,\!9\cdot 1,\!9}{6} 0,\!0000008=3,\!0004341 $$

MATH

A maradék-tag képlete:

$$R_3(x)=h^4\frac{f^{(4)}(\xi)}{4!}t(t-1)(t-2)(t-3)$$

ahol $1000<\xi <1030.$

Mivel

$$f^{(4)}(x)= -\frac{3!}{x^4}\lg e$$

akkor

$$|f^{(4)}(\xi)|<\frac{3!}{1000^4}\lg e,$$

és

$$|R_3(x)|=\frac{0,\!1\cdot 0,\!9\cdot 1,\!9\cdot 2,\!9\cdot 10^4\lg e}{4\cdot 1000^4}\approx 0,\!5\cdot 10^{-9}.$$

3.7. Példa

A $y=\displaystyle\frac{1}{x}$ függvény táblázat formában van megadva. Lineáris interpoláció segítségével számítsuk ki a $\displaystyle\frac{1}{2,\!718}$ értékét.

$$\begin{matrix} x & y & \Delta y \\ 2,\!70 & 0,\!3704 & -0,\!0028 \\ 2,\!72 & 0,\!3676 & -0,\!0026 \\ 2,\!74 & 0,\!3650 & \\ \end{matrix} $$

$$t=\frac{x-x_0}{h}=\frac{2,\!718-2,\!70}{0,\!2}=0,\!9.$$

Akkor

$$\frac{1}{2,\!718}=0,\!3704-0,\!0028\cdot0,\!9=0,\!3679.$$

A maradék-tag becslése:

$$R_1(x)=h^2\frac{f^{(2)}(\xi)}{2!}t(t-1)\quad 2,\!70<\xi <2,\!72$$

$$f^{(2)}(x)=\frac{2}{x^3},$$

és

$$|R_1(2,\!718)|=\frac{(0,\!02)^2\cdot 0,\!9\cdot 0,\!1}{2,\!7^3}\approx 0,\!2\cdot 10^{-5}.$$

3.8. Példa

Adva van a $y=e^{x}$ függvény táblázat formában. Kvadratikus interpoláció segítségével számítsuk ki a $e^{3,62}$ és $e^{3,62}$ értékeket.

$$\begin{matrix} x & y & \Delta y & \Delta^2y \\ 3,\!60 & 36,\!598 & 1,\!877 & 0,\!095 \\ 3,\!65 & 38,\!475 & 1,\!972 & 0,\!102 \\ 3,\!70 & 40,\!447 & 2,\!074 \\ 3,\!75 & 42,\!521 & \\ \end{matrix} $$

a) $x=3,\!62,\quad t=\displaystyle\frac{0,\!02}{0,\!05}=0,\!4$

$$e^{3,62}=y_0+t\Delta y_0+\frac{t(t-1)}{2!}\Delta^2y_0=36,\!598+0,\!4\cdot 1,\!877-\frac{0,\!4\cdot 0,\!6}{2}0,\!095=37,\!338 $$

A maradék-tag becslése:

$$R_2(x)=h^3\frac{f^{(3)}(\xi)}{3!}t(t-1)(t-2),\quad 3,\!60<\xi <3,\!70$$

$$|R_2(3,\!62)|=\frac{(0,\!05)^3\cdot 0,\!4\cdot 0,\!6\cdot 1,\!6}{6}e^{3,70}\approx 0,\!3\cdot 10^{-3}.$$

b) $x=3,\!58,\quad t=-\displaystyle\frac{0,\!02}{0,\!05}=-0,\!4$

$$e^{3,58}=y_0+t\Delta y_0+\frac{t(t-1)}{2!}\Delta^2y_0=36,\!598+0,\!4\cdot 1,\!877-\frac{0,\!4\cdot 1,\!6}{2}0,\!095=35,\!874 $$

A maradék-tag becslése:

$$R_2(3,\!58)<\frac{(0,\!05)^3\cdot 0,\!4\cdot 1,\!4\cdot 2,\!4}{6}e^{3,70}\approx 10^{-3}.$$

Ha az alappontokat a következő sorrendben fogjuk alkalmazni a Newton-féle interpolációs polinomban:

$$x_n,x_{n-1},\ldots, x_1, x_0$$

akkor megkapjuk a második Newton-féle interpolációs polinomot:

$$N^{(2)}_n(x)=y_n+t\Delta y_{n-1}+\frac{t(t-1)}{2!}\Delta^2y_{n-1}+\ldots+\frac{t(t+1)\ldots(t+(n-1))}{n!}\Delta^ny_0 x\tag{3.81}\label{eq:3.81}$$ (3.81)

ahol

$$t=\frac{x-x_0}{h},$$

A mardék-tag képlete: $$\boxed{R_n(x)=h^{n+1}t(t+1)\ldots(t+n)\frac{f^{(n+1)}(\xi)}{(n+1)!} } \tag{3.82}\label{eq:3.82}$$ (3.81)

Az első Newton-féle interpolációs polinom hiba-becslése a $x_0$ pont közelében a legkisebb, a második Newton-féle interpolációs polinom hiba-becslése pedig – a $x_n$ pont közelében a legkisebb.

3.9. Példa

Adva van a $y=\sin x$ függvény táblázata.

Számítsuk ki a $\sin 54^\circ$ és a $\sin 56^\circ$ értékeket.

$$\begin{matrix} x & y & \Delta y & \Delta^2y & \Delta^3y \\ 30^\circ & 0,\!5000 & 0,\!0736 & -0,\!0044 & -0,\!0005 \\ 35^\circ & 0,\!5736 & 0,\!0692 & -0,\!0049 & -0,\!0005 \\ 40^\circ & 0,\!6428 & 0,\!0643 & -0,\!0054 & -0,\!0003 \\ 45^\circ & 0,\!7071 & 0,\!0589 & -0,\!0057 & \\ 50^\circ & 0,\!7660 & 0,\!0532 & & \\ 55^\circ & 0,\!8192 & & & \\ \end{matrix} $$

a) $\sin 54^\circ\quad t=\displaystyle\frac{54-55}{5}=-0,\!2$

$$\sin 54^\circ=y_n+t\Delta y_{n-1}+\frac{t(t+1)}{2!}\Delta^2y_{n-2}+\frac{t(t+1)(t+2)}{3!}\Delta^3y_{n-3}+\ldots+\frac{t(t+1)\ldots(t+(n-1))}{n!}\Delta^ny_0+ $$

$$=0,\!8192+(-0,\!2)0,\!0532-\frac{(-0,\!2)\cdot 0,\!8}{2}0,\!0057-\frac{(-0,\!2)\cdot 0,\!8\cdot 1,\!8}{6}0,\!0003=0,\!80903 $$

Hiba-becslés:

$$R_3(x)=h^4\frac{t(t+1)(t+2)(t+3)}{4!}f^{(4)}(\xi)$$

$$h=5^\circ=0,\!0873,\quad t=-0,\!2,\quad f^{(4)}(\xi)=\sin\xi\leqslant 1$$

$$|R_3(54)|\leqslant\frac{(0,\!087)^4}{24}0,\!2\cdot 0,\!8\cdot 1,\!8\cdot 2,\!8\cdot\approx 0,\!2\cdot 10^{-5}$$

b) $\sin 56^\circ\quad t=\displaystyle\frac{56-55}{5}=0,\!2$

$$\sin 56^\circ=y_n+t\Delta y_{n-1}+\frac{t(t+1)}{2!}\Delta^2y_{n-2}+\frac{t(t+1)(t+2)}{3!}\Delta^3y_{n-3}+\ldots+\frac{t(t+1)\ldots(t+(n-1))}{n!}\Delta^ny_0+ $$

$$=0,\!8192+0,\!2\cdot 0,\!0532-\frac{0,\!2\cdot 0,\!8}{2}0,\!0057-\frac{0,\!2\cdot 0,\!8\cdot 1,\!8}{6}0,\!0003=0,\!82913 $$

Hiba-becslés:

$$R_3(x)=h^4\frac{t(t+1)(t+2)(t+3)}{4!}f^{(4)}(\xi)$$

$$h=5^\circ=0,\!0873,\quad t=0,\!2,\quad f^{(4)}(\xi)=\sin\xi\leqslant 1$$

$$|R_3(56)|\leqslant\frac{(0,\!087)^4}{24}0,\!2\cdot 1,\!2\cdot 2,\!2\cdot 3,\!2\cdot\approx 0,\!4\cdot 10^{-5}$$

Javasoljuk megoldani a 10. Fejezetben található feladatokat.

Ha az $f(x)$ függvény monoton, akkor létezik inverz Lagrange-féle interpolációs polinom, amelyet könnyen kapjuk, ha a $\eqref{eq:3.23}$ (3.23) képletben az $x$ és $y$ értékek kölcsönösen becseréljük:

$$x=\sum_{i=0}^n=\frac{(y-y_0)(y-y_1)\cdot\ldots(y-y_{i-1})(y-y_{i+1})\cdot\ldots(y-y_n)} {(y_i-y_0)(y_i-y_1)\cdot\ldots(y_i-y_{i-1})(y_i-y_{i+1})\cdot\ldots(y_i-y_n)}\cdot x_i \tag{3.83}\label{eq:3.83}$$ MATH (3.81)

9.Példa

$$\begin{array}{|c|c|c|c|c|} \hline X & 10 & 15 & 17 & 20 \\ \hline Y & 3 & 7 & 11 & 17 \\ \hline \end{array}$$

$$y=10,\quad x=?$$

$$x=\sum_{i=0}^3L_i^{(3)}(y_i)\cdot x_i$$

$$x(10)=10\frac{(10-7)(10-11)(10-17)}{(3-7)(3-11)(3-17)} +15\frac{(10-3)(10-11)(10-17)}{(7-3)(7-11)(7-17)}+$$

$$+17\frac{(10-3)(10-7)(10-17)}{(11-3)(11-7)(11-17)}+ 20\frac{(10-3)(10-17)(10-11)}{(17-3)(17-7)(17-11)}=16,\!641. $$

Javasoljuk megoldani a 10. Fejezetben található feladatokat.

Egyenletek megoldása inverz interpoláció alkalmazásával.

10. Példa

$$e^{(-x)}-x=0, \quad f(x)=e^{(-x)}-x.$$

$$\begin{array}{|c|c|c|c|c|} \hline x & 0,\!50 & 0,\!55 & 0,\!60 & 0,\!65 & 0,\!70 \\ \hline Y & 0,\!10653 & 0,\!02695 & -0,\!05119 & -0,\!12795 & -0,\!20342 \\ \hline \end{array}$$

$$y=0,\quad x=?$$

$$x=0,\!56724$$

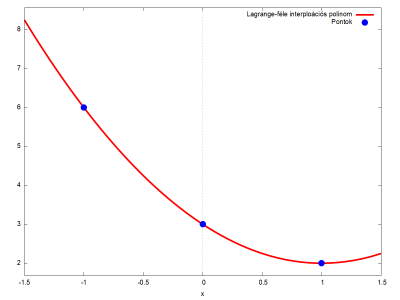
Lagrange-féle interpoláció. Első változat.

x0:-1$ x1:0$ x2:1$

y0:6$ y1:3$ y2:2$;

f0:(x-x1)*(x-x2); f1:(x-x0)*(x-x2); f2:(x-x0)*(x-x1);

$(x-1)\cdot x\\ (x-1)\cdot (x+1)\\ x\cdot (x+1)$

g0:(x0-x1)*(x0-x2); g1:(x1-x0)*(x1-x2); g2:(x2-x0)*(x2-x1);

$2\\-1\\2$

L3:f0*y0/g0+f1*y1/g1+f2*y2/g2;

$x\cdot (x+1)-3\cdot (x-1)\cdot (x+1)+3\cdot (x-1)\cdot x$

expand(L3);

$x^2-2\cdot x+3$

L3, x=1.5;

$2.25$

Lagrange-féle interpoláció. Második változat.

xy:[[-1,6],[0,3],[1,2]];

[[-1,6],[0,3],[1,2]]

f0:(x-xy[2][1])*(x-xy[3][1]);f1:(x-xy[1][1])*(x-xy[3][1]);f2:(x-xy[1][1])*(x-xy[2][1]);

$(x-1)\cdot x \\(x-1)\cdot(x+1) \\x\cdot(x+1)$

g0:(xy[1][1]-xy[2][1])*(xy[1][1]-xy[3][1]);g1:(xy[2][1]-xy[1][1])*(xy[2][1]-xy[3][1]);g2:(xy[3][1]-xy[1][1])*(xy[3][1]-xy[2][1]);

$2\\-1\\2$

L3:f0*xy[1][2]/g0+f1*xy[2][2]/g1+f2*xy[3][2]/g2;

$x\cdot(x+1)-3\cdot(x-1)\cdot(x+1)+3\cdot(x-1)\cdot x$

expand(%);

$x^2-2\cdot x+3$

%, x=1.5;

$2.25$

Lagrange-féle interpoláció. Harmadik változat.

load(interpol)$

xy:[[-1,6],[0,3],[1,2]];

[[-1,6],[0,3],[1,2]]

L3:lagrange(xy);

$x\cdot (x+1)-3\cdot(x-1)\cdot(x+1)+3\cdot(x-1)\cdot x$

expand(%);

$x^2-2\cdot x+3$

L3,x=1.5;

2.25

wxplot2d([L3,[discrete,xy]],[x,-1.5,1.5],[style,[lines,5,2],[points,6,1,1]],[legend,"Lagrange-féle interploációs polinom","Pontok"]);